



Nächste Seite: Erweiterung des
Poincaré-Schnitts auf Aufwärts: Beispiel für ein einfaches Vorherige Seite: Beispiel für ein einfaches Inhalt
Delay in der logistischen Gleichung
Um sich einen Eindruck zu verschaffen, welchen Einfluss die Einführung eines
Delays hat, soll an dieser Stelle die logistische Gleichung als ein Beispiel
betrachtet werden.
Die zeitdiskrete logistische Gleichung
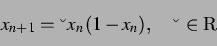
|
(55) |
ist ein gut untersuchtes und gut verstandenes Standardbeispiel für ein
nichtlineares System mit chaotischen Lösungen. Man findet bei ihr die
charakteristischen Eigenschaften nichtlinearer Systeme. Über eine
Periodenverdopplungskaskade führt sie für sukzessive Erhöhung des
Parameters  ins Chaos ([16]).
ins Chaos ([16]).
Die kontinuierliche logistische Gleichung
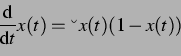 |
(56) |
dagegen verhält sich völlig unchaotisch und monoton, denn für das
Auftreten von Oszillationen in kontinuierlichen Systemen benötigt man ein System
von mindestens zwei Differentialgleichungen erster Ordnung. Um chaotisches Verhalten
zu beobachten, benötigt man mindestens drei ([13]). Eine Delaydifferentialgleichung ist nun
im Prinzip unendlichdimensional, so dass auch bei nur einer abhängigen Variablen
komplexes Verhalten und Chaos auftreten können.
Es gibt mehrere Möglichkeiten, die Gleichung (B.2) zu einer Delaydifferentialgleichung zu erweitern.
Eine von SAATY et al. in [32]
untersuchte Form ist
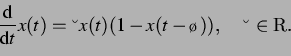
|
(57) |
Laut SAATY kann diese Gleichung nun alle Verhaltensweisen
nichtlinearer Gleichungen zeigen.
- monotones Verhalten wie bei der kontinuierlichen logistischen Gleichung ohne
Delay für
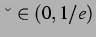
- Oszillieren um ein Gleichgewicht für
![$\lambda \in [1/e,\pi/2]$](img571.png)
- chaotisches Verhalten für
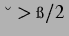
Diese Eigenschaften konnten mit dem hier verwendeten numerischen Löser gut
nachgewiesen werden. Allerdings wurde bei den Rechnungen in dieser Arbeit kein Chaos,
wie es von BAKER et al. beschrieben wurde, ,,nicht charakteristische
Muster``, wie von SAATY et al. behauptet, für
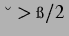 gefunden, sondern periodische Schwingungen mit hohen
Amplituden (vgl. Abb. B.1.
gefunden, sondern periodische Schwingungen mit hohen
Amplituden (vgl. Abb. B.1.
Abbildung B.1: Keine chaotische Schwingung für
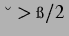 bei einem Startwert von
bei einem Startwert von  ; entgegen den
Angaben von SAATY.
; entgegen den
Angaben von SAATY.
|
|
Es wurde noch eine weitere, von (B.3)
abweichende Form der kontinuierlichen logistischen Delaygleichung betrachtet:
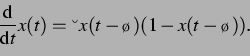
|
(58) |
Im folgenden sollen nun einige Eigenschaften dieser Gleichung untersucht werden. Wie
die Abbildungen B.2 und B.3 zeigen ist bei einem Delay von 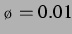 bei
bei  noch kein Unterschied zu sehen.
noch kein Unterschied zu sehen.
Abbildung: Lösung der logistischen Gleichung für
sehr kleines Delay 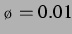 (links) ohne Delay (rechts) bei
(links) ohne Delay (rechts) bei  . Es ist kein Unterschied zu sehen.
. Es ist kein Unterschied zu sehen.
|
|
Abbildung: Lösung der logistischen Gleichung für
sehr kleines Delay 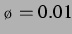 (links) ohne Delay (rechts) bei
(links) ohne Delay (rechts) bei  . Es ist kein Unterschied zu sehen.
. Es ist kein Unterschied zu sehen.
|
|
Abbildung: Lösung der logistischen Gleichung für
sehr kleines Delay 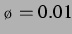 (links) ohne Delay (rechts) bei
(links) ohne Delay (rechts) bei
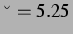 . Es ist kein Unterschied zu sehen.
. Es ist kein Unterschied zu sehen.
|
|
Erhöht man nun das Delay auf 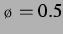 , beginnt das System ein etwas
komplexeres Verhalten zu zeigen. Die Abbildungen B.5 bis B.9
zeigen, dass die Lösung für wachsendes
, beginnt das System ein etwas
komplexeres Verhalten zu zeigen. Die Abbildungen B.5 bis B.9
zeigen, dass die Lösung für wachsendes
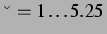 zunächst monoton verläuft (Abb. B.5), sich dann langsam aufschaukelt (Abb. B.6 und B.7)
und schließlich in ein periodisches ungedämpftes Verhalten übergeht
(Abb. B.8 und B.9). Erhöht man
zunächst monoton verläuft (Abb. B.5), sich dann langsam aufschaukelt (Abb. B.6 und B.7)
und schließlich in ein periodisches ungedämpftes Verhalten übergeht
(Abb. B.8 und B.9). Erhöht man  noch weiter divergiert die
Lösung nach
noch weiter divergiert die
Lösung nach 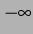 . Es wurde eine Art Phasendiagramm erstellt und in
Abbildung B.10 dargestellt.
. Es wurde eine Art Phasendiagramm erstellt und in
Abbildung B.10 dargestellt.
Abbildung: Lösung der logistischen Gleichung für
 und
und 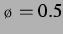 (links) ohne Delay (rechts): monotones
Verhalten (mit leichtem Überschwingen bei
(links) ohne Delay (rechts): monotones
Verhalten (mit leichtem Überschwingen bei 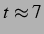 ).
).
|
|
Abbildung: Lösung der logistischen Gleichung für
 und
und 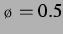 (links) ohne Delay (rechts). Die Schwingung
beginnt, ist aber noch sehr stark gedämpft.
(links) ohne Delay (rechts). Die Schwingung
beginnt, ist aber noch sehr stark gedämpft.
|
|
Abbildung: Lösung der logistischen Gleichung für
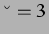 und
und 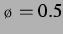 (links) ohne Delay (rechts). Die Dämpfung
nimmt gegenüber Abbildung B.6
deutlich ab.
(links) ohne Delay (rechts). Die Dämpfung
nimmt gegenüber Abbildung B.6
deutlich ab.
|
|
Abbildung: Lösung der logistischen Gleichung für
 und
und 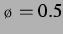 (links) ohne Delay (rechts). Die Lösung
schwingt periodisch mit
(links) ohne Delay (rechts). Die Lösung
schwingt periodisch mit 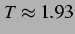 .
.
|
|
Abbildung: Lösung der logistischen Gleichung für
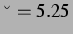 und
und 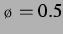 (links) ohne Delay (rechts). Nicht
sinusförmige, periodische Lösung mit
(links) ohne Delay (rechts). Nicht
sinusförmige, periodische Lösung mit 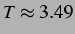 .
.
|
|
Abbildung B.10: Gestrichelt: 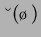 -Kurve, bei der
das monotone Verhalten der Lösung endet. Durchgezogen:
-Kurve, bei der
das monotone Verhalten der Lösung endet. Durchgezogen: 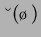 -Kurve, oberhalb derer die Lösung divergiert. Somit
umfasst der Bereich zwischen den Kurven sowohl den gedämpft schwingenden
Lösungsraum als auch den Bereich, in dem periodische Lösungen
auftreten. Im rechten Bild sind die Werte doppelt-logarithmisch aufgetragen.
Der
-Kurve, oberhalb derer die Lösung divergiert. Somit
umfasst der Bereich zwischen den Kurven sowohl den gedämpft schwingenden
Lösungsraum als auch den Bereich, in dem periodische Lösungen
auftreten. Im rechten Bild sind die Werte doppelt-logarithmisch aufgetragen.
Der  -Wert für den Beginn der Schwingung und der für den
Beginn der Divergenz folgen also einem
-Wert für den Beginn der Schwingung und der für den
Beginn der Divergenz folgen also einem 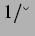 Gesetz. Dies lässt
sich sicherlich auch durch eine Stabilitätsanalyse von Gleichung (B.4) zeigen, ist jedoch nicht Ziel dieser
Arbeit.
Gesetz. Dies lässt
sich sicherlich auch durch eine Stabilitätsanalyse von Gleichung (B.4) zeigen, ist jedoch nicht Ziel dieser
Arbeit.
|
|




Nächste Seite: Erweiterung des
Poincaré-Schnitts auf Aufwärts: Beispiel für ein einfaches Vorherige Seite: Beispiel für ein einfaches Inhalt
Stefan Kamphausen 2003-07-17
![\includegraphics [width=5cm,angle=-90]{saaty_wrong.ps}](img572.png)
![\includegraphics [width=5cm,angle=-90]{logi_d_0.01_1.ps}](img574.png)
![\includegraphics [width=5cm,angle=-90]{logi_n_0.01_1.ps}](img575.png)
![\includegraphics [width=5cm,angle=-90]{logi_d_0.01_4.ps}](img576.png)
![\includegraphics [width=5cm,angle=-90]{logi_n_0.01_4.ps}](img577.png)
![\includegraphics [width=5cm,angle=-90]{logi_d_0.01_5.25.ps}](img578.png)
![\includegraphics [width=5cm,angle=-90]{logi_n_0.01_5.25.ps}](img579.png)
![]() , beginnt das System ein etwas
komplexeres Verhalten zu zeigen. Die Abbildungen B.5 bis B.9
zeigen, dass die Lösung für wachsendes
, beginnt das System ein etwas
komplexeres Verhalten zu zeigen. Die Abbildungen B.5 bis B.9
zeigen, dass die Lösung für wachsendes
![]() zunächst monoton verläuft (Abb. B.5), sich dann langsam aufschaukelt (Abb. B.6 und B.7)
und schließlich in ein periodisches ungedämpftes Verhalten übergeht
(Abb. B.8 und B.9). Erhöht man
zunächst monoton verläuft (Abb. B.5), sich dann langsam aufschaukelt (Abb. B.6 und B.7)
und schließlich in ein periodisches ungedämpftes Verhalten übergeht
(Abb. B.8 und B.9). Erhöht man ![]() noch weiter divergiert die
Lösung nach
noch weiter divergiert die
Lösung nach ![]() . Es wurde eine Art Phasendiagramm erstellt und in
Abbildung B.10 dargestellt.
. Es wurde eine Art Phasendiagramm erstellt und in
Abbildung B.10 dargestellt.![\includegraphics [width=5cm,angle=-90]{logi_d_1.ps}](img582.png)
![\includegraphics [width=5cm,angle=-90]{logi_n_1.ps}](img583.png)
![\includegraphics [width=5cm,angle=-90]{logi_d_2.ps}](img584.png)
![\includegraphics [width=5cm,angle=-90]{logi_n_2.ps}](img585.png)
![\includegraphics [width=5cm,angle=-90]{logi_d_3.ps}](img586.png)
![\includegraphics [width=5cm,angle=-90]{logi_n_3.ps}](img587.png)
![\includegraphics [width=5cm,angle=-90]{logi_d_4.ps}](img588.png)
![\includegraphics [width=5cm,angle=-90]{logi_n_4.ps}](img589.png)
![\includegraphics [width=5cm,angle=-90]{logi_d_5.25.ps}](img590.png)
![\includegraphics [width=5cm,angle=-90]{logi_n_5.25.ps}](img591.png)
![\includegraphics [width=5cm,angle=-90]{logi_schwing.ps}](img592.png)
![\includegraphics [width=5cm,angle=-90]{logi_schwing_log.ps}](img593.png)