



Nächste Seite: Ergebnisse
Aufwärts: Die linearisierte
Keller-Miksis-Gleichung ohne Vorherige Seite: Die linearisierte Keller-Miksis-Gleichung ohne Inhalt
Theorie
Für Blasen, für deren Ruheradius 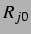
 gilt, und bei geringem
Anregungsdruck
gilt, und bei geringem
Anregungsdruck
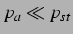 gilt die linearisierte Form der Keller-Miksis-Gleichung (der
Einfachheit halber in komplexer Schreibweise):
gilt die linearisierte Form der Keller-Miksis-Gleichung (der
Einfachheit halber in komplexer Schreibweise):
Man kann aus der Beziehung zwischen  und
und 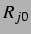 (3.3) entweder den linearen Resonanzradius
(3.3) entweder den linearen Resonanzradius
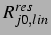 (Minneart'scher Radius [26]) bei gegebenem
(Minneart'scher Radius [26]) bei gegebenem  oder aber zu einem
oder aber zu einem 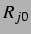 die
lineare Resonanzfrequenz
die
lineare Resonanzfrequenz
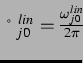 berechnen. Für diese beiden
Größen gilt bei Vernachlässigung der Oberflächenspannung
berechnen. Für diese beiden
Größen gilt bei Vernachlässigung der Oberflächenspannung 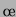 und
bei Normalbedingungen in Wasser die Faustregel
und
bei Normalbedingungen in Wasser die Faustregel
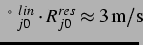 . Somit ergibt sich also
für den linearen Resonanzradius bei der hier durchgehend verwendeten
Anregungsfrequenz von
. Somit ergibt sich also
für den linearen Resonanzradius bei der hier durchgehend verwendeten
Anregungsfrequenz von
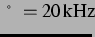 :
:
durch explizites Auflösen von Gleichung (3.3) nach 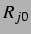 :
:
Nun soll Gleichung (3.2), die einen
getriebenen, gedämpften harmonischen Oszillator beschreibt, gelöst
werden.
Ansatz:
Einsetzen in (3.2) und Teilen durch
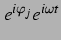 ergibt:
ergibt:
Von dieser Gleichung der Realteil und der Imaginärteil betrachtet, ergibt ein
Gleichungssystem:
Quadrieren und Addieren der beiden Gleichungen (3.7) und (3.8) liefert
nach Umstellen:
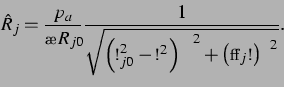
|
(26) |
Teilt man hingegen die beiden Gleichungen durcheinander, erhält man:
Damit ergibt sich die Schwingung als Realteil des Ansatzes (3.4) zu:
Also schwingt die Blase gemäß
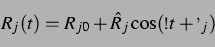
|
(29) |
mit einem
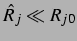 . Es ergibt sich dann für das Volumen der
. Es ergibt sich dann für das Volumen der 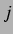 -ten Blase:
-ten Blase:
für die Ableitung:
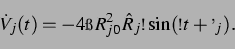
|
(32) |
Eingesetzt in die Gleichung (2.11)
erhält man dann für die sekundäre Bjerkneskraft:
Mit Hilfe der Beziehung
(s. [8]; dieses Buch darf nicht
unerwähnt bleiben) und aufgrund des verschwindenden Integrals
erhält man die sekundäre Bjerkneskraft im linearen Fall zu:
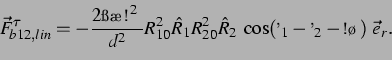
|
(34) |
Dabei berechnen sich die 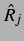 und
und 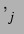 nach Gl. (3.9) und Gl. (3.10). [Dies ist konsistent mit Gleichung (2.12), wobei hier eine Radiusschwingung betrachtet
wird, in Gl. (2.12) dagegen eine
Volumenschwingung.]
nach Gl. (3.9) und Gl. (3.10). [Dies ist konsistent mit Gleichung (2.12), wobei hier eine Radiusschwingung betrachtet
wird, in Gl. (2.12) dagegen eine
Volumenschwingung.]
Da das Delay 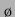 im Argument des Kosinus auftaucht, ist es sinnvoll, das Delay in
Bruchteilen der Periodendauer
im Argument des Kosinus auftaucht, ist es sinnvoll, das Delay in
Bruchteilen der Periodendauer
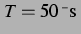 zu messen. So wurden für verschiedene feste
Anregungsdruckamplituden
zu messen. So wurden für verschiedene feste
Anregungsdruckamplituden 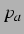 , deren Größe die Nichtlinearität in der
Keller-Miksis-Gleichung bestimmt, Serien verschiedener
, deren Größe die Nichtlinearität in der
Keller-Miksis-Gleichung bestimmt, Serien verschiedener 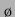 berechnet. Dabei wurde
jedesmal
berechnet. Dabei wurde
jedesmal 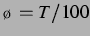 für ein sehr kleines Delay gewählt und
für ein sehr kleines Delay gewählt und 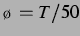 , um die
Dynamik von sehr kleinem Delay zu größerem aufzuzeigen, falls diese
bemerkenswert erschien. Delaywerte von
, um die
Dynamik von sehr kleinem Delay zu größerem aufzuzeigen, falls diese
bemerkenswert erschien. Delaywerte von 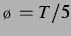 ,
, 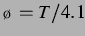 ,
, 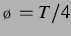 und
und 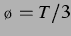 zeigen die
Entwicklung um den ,,unsymmetrischsten`` Punkt bei
zeigen die
Entwicklung um den ,,unsymmetrischsten`` Punkt bei 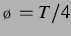 , an dem die in [25] beobachtete Symmetrie bei Blasenvertauschung im
nicht delay-gekoppelten Fall am wenigsten wiederzufinden ist. Als letzter Wert jeder
Serie zeigt
, an dem die in [25] beobachtete Symmetrie bei Blasenvertauschung im
nicht delay-gekoppelten Fall am wenigsten wiederzufinden ist. Als letzter Wert jeder
Serie zeigt 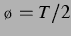 die Invertierung von
die Invertierung von 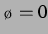 durch Verschiebung der Phase des
abgestrahlten Schallfeldes um
durch Verschiebung der Phase des
abgestrahlten Schallfeldes um 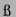 . Dies ist der größte untersuchte Delaywert.
Was ein ,,großes`` Delay ist, hängt allerdings stark von der
Anregungsfrequenz ab, von der Periodenlänge der Blasenschwingung im
Verhältnis zur Laufzeit des Schalls, bis er auf vernachlässigbare
Größe abgeklungen ist. Bei höheren Frequenzen können durchaus
. Dies ist der größte untersuchte Delaywert.
Was ein ,,großes`` Delay ist, hängt allerdings stark von der
Anregungsfrequenz ab, von der Periodenlänge der Blasenschwingung im
Verhältnis zur Laufzeit des Schalls, bis er auf vernachlässigbare
Größe abgeklungen ist. Bei höheren Frequenzen können durchaus
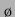 -Werte interessant sein, die ein Vielfaches von
-Werte interessant sein, die ein Vielfaches von 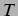 betragen.
betragen.
Die sekundäre Bjerkneskraft der ersten auf die zweite Blase gemäß
Gleichung (3.17) wird in den folgenden
Abbildungen, die die 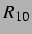 -
-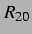 -Ebene zeigen, in z-Richtung aufgetragen und auf der linken
Seite als Gebirgsplot mit der Projektion der Nulldurchgangslinie gezeigt. Der
vektorielle Charakter der Kraft findet dabei keine Berücksichtigung; es ist
immer die Kraft in positive
-Ebene zeigen, in z-Richtung aufgetragen und auf der linken
Seite als Gebirgsplot mit der Projektion der Nulldurchgangslinie gezeigt. Der
vektorielle Charakter der Kraft findet dabei keine Berücksichtigung; es ist
immer die Kraft in positive 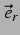 -Richtung gemeint, es ist in den Abbildungen
-Richtung gemeint, es ist in den Abbildungen
dargestellt. Der Ausschnitt aus der 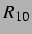 -
-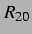 -Ebene zwischen
-Ebene zwischen
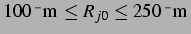 wurde gewählt, da sich der
lineare Resonanzradius etwa in der Mitte dieses Ausschnitts befindet, und in dessen
Nähe die bedeutenden Beobachtungen an der Dynamik zu erwarten sind. In allen
wesentlichen Arbeiten zu diesem Thema wurde ebenfalls starkes Augenmerk auf das
Vorzeichen der sekundären Bjerkneskraft gelegt, so dass es sinnvoll erscheint,
dies auch hier zu tun, damit die Unterschiede zu bisherigen Theorien, die sich durch
das Delay ergeben, deutlich gemacht werden. Daher ist rechts in der Abbildung das zur
Bjerkneskraft gehörende Vorzeichen abgebildet. Dabei bedeutet schwarz eine
negative Kraft, also Anziehung, und weiß eine positive, also Abstoßung.
Für das Partikelmodell ist das Vorzeichen der sekundären Bjerkneskraft von
besonderem Interesse. Wird beispielsweise die erste Blase von der zweiten angezogen,
die zweite aber von der ersten abgestoßen, laufen sie zusammen in eine
Richtung, und dieses Verhalten könnte für das Auftreten von Streamern mit
verantwortlich sein.
wurde gewählt, da sich der
lineare Resonanzradius etwa in der Mitte dieses Ausschnitts befindet, und in dessen
Nähe die bedeutenden Beobachtungen an der Dynamik zu erwarten sind. In allen
wesentlichen Arbeiten zu diesem Thema wurde ebenfalls starkes Augenmerk auf das
Vorzeichen der sekundären Bjerkneskraft gelegt, so dass es sinnvoll erscheint,
dies auch hier zu tun, damit die Unterschiede zu bisherigen Theorien, die sich durch
das Delay ergeben, deutlich gemacht werden. Daher ist rechts in der Abbildung das zur
Bjerkneskraft gehörende Vorzeichen abgebildet. Dabei bedeutet schwarz eine
negative Kraft, also Anziehung, und weiß eine positive, also Abstoßung.
Für das Partikelmodell ist das Vorzeichen der sekundären Bjerkneskraft von
besonderem Interesse. Wird beispielsweise die erste Blase von der zweiten angezogen,
die zweite aber von der ersten abgestoßen, laufen sie zusammen in eine
Richtung, und dieses Verhalten könnte für das Auftreten von Streamern mit
verantwortlich sein.




Nächste Seite: Ergebnisse
Aufwärts: Die linearisierte
Keller-Miksis-Gleichung ohne Vorherige Seite: Die linearisierte Keller-Miksis-Gleichung ohne Inhalt
Stefan Kamphausen 2003-07-17
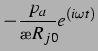
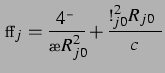
![$\displaystyle \omega_{j0}^2 = \frac{1}{\rho R_{j0}^2}\left[3\kappa p_{st}+\frac{2\sigma}{R_{j0}}(3\kappa-1)\right].$](img185.png)
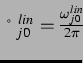 berechnen. Für diese beiden
Größen gilt bei Vernachlässigung der Oberflächenspannung
berechnen. Für diese beiden
Größen gilt bei Vernachlässigung der Oberflächenspannung 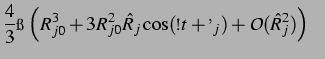
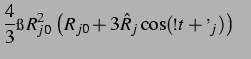
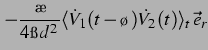
![$\displaystyle -\frac{\rho(4\pi \omega)^2}{4\pi d^2} R_{10}^2 \hat{R}_{1} R_{20}... ... (t-\tau) +\varphi_1\right]\, \sin\left[\omega t +\varphi_2\right]}\, \vec{e}_r$](img227.png)
![$\displaystyle - \frac{4\pi\rho\omega^2}{d^2} R_{10}^2 \hat{R}_{1} R_{20}^2 \hat... ... +\varphi_1\right] \, \sin\left[\omega t +\varphi_2\right]\;\diff t\,\vec{e}_r.$](img228.png)
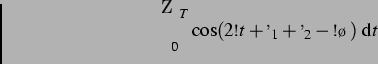
![]() im Argument des Kosinus auftaucht, ist es sinnvoll, das Delay in
Bruchteilen der Periodendauer
im Argument des Kosinus auftaucht, ist es sinnvoll, das Delay in
Bruchteilen der Periodendauer
![]() zu messen. So wurden für verschiedene feste
Anregungsdruckamplituden
zu messen. So wurden für verschiedene feste
Anregungsdruckamplituden ![]() , deren Größe die Nichtlinearität in der
Keller-Miksis-Gleichung bestimmt, Serien verschiedener
, deren Größe die Nichtlinearität in der
Keller-Miksis-Gleichung bestimmt, Serien verschiedener ![]() berechnet. Dabei wurde
jedesmal
berechnet. Dabei wurde
jedesmal ![]() für ein sehr kleines Delay gewählt und
für ein sehr kleines Delay gewählt und ![]() , um die
Dynamik von sehr kleinem Delay zu größerem aufzuzeigen, falls diese
bemerkenswert erschien. Delaywerte von
, um die
Dynamik von sehr kleinem Delay zu größerem aufzuzeigen, falls diese
bemerkenswert erschien. Delaywerte von ![]() ,
, ![]() ,
, ![]() und
und ![]() zeigen die
Entwicklung um den ,,unsymmetrischsten`` Punkt bei
zeigen die
Entwicklung um den ,,unsymmetrischsten`` Punkt bei ![]() , an dem die in [25] beobachtete Symmetrie bei Blasenvertauschung im
nicht delay-gekoppelten Fall am wenigsten wiederzufinden ist. Als letzter Wert jeder
Serie zeigt
, an dem die in [25] beobachtete Symmetrie bei Blasenvertauschung im
nicht delay-gekoppelten Fall am wenigsten wiederzufinden ist. Als letzter Wert jeder
Serie zeigt ![]() die Invertierung von
die Invertierung von ![]() durch Verschiebung der Phase des
abgestrahlten Schallfeldes um
durch Verschiebung der Phase des
abgestrahlten Schallfeldes um ![]() . Dies ist der größte untersuchte Delaywert.
Was ein ,,großes`` Delay ist, hängt allerdings stark von der
Anregungsfrequenz ab, von der Periodenlänge der Blasenschwingung im
Verhältnis zur Laufzeit des Schalls, bis er auf vernachlässigbare
Größe abgeklungen ist. Bei höheren Frequenzen können durchaus
. Dies ist der größte untersuchte Delaywert.
Was ein ,,großes`` Delay ist, hängt allerdings stark von der
Anregungsfrequenz ab, von der Periodenlänge der Blasenschwingung im
Verhältnis zur Laufzeit des Schalls, bis er auf vernachlässigbare
Größe abgeklungen ist. Bei höheren Frequenzen können durchaus
![]() -Werte interessant sein, die ein Vielfaches von
-Werte interessant sein, die ein Vielfaches von ![]() betragen.
betragen.![]() -
-![]() -Ebene zeigen, in z-Richtung aufgetragen und auf der linken
Seite als Gebirgsplot mit der Projektion der Nulldurchgangslinie gezeigt. Der
vektorielle Charakter der Kraft findet dabei keine Berücksichtigung; es ist
immer die Kraft in positive
-Ebene zeigen, in z-Richtung aufgetragen und auf der linken
Seite als Gebirgsplot mit der Projektion der Nulldurchgangslinie gezeigt. Der
vektorielle Charakter der Kraft findet dabei keine Berücksichtigung; es ist
immer die Kraft in positive ![]() -Richtung gemeint, es ist in den Abbildungen
-Richtung gemeint, es ist in den Abbildungen