



Nächste Seite: Keller-Miksis-Modell Aufwärts: Strukturbildung bei Kavitationsblasen Vorherige Seite:
Strukturbildung bei Kavitationsblasen
Inhalt
Die sekundäre Bjerkneskraft
Es soll nun die Formel für die Berechnung der sekundären Bjerkneskraft
hergeleitet werden. Es werden zwei Kavitationsblasen in einem stationären
Schallfeld betrachtet, dessen Wellenlänge groß ist gegen den Abstand der
Blasenmittelpunkte und dieser wiederum groß gegen die Blasenradien. Somit wird
also zunächst angenommen, dass Phase und Amplitude des Schalldrucks für
beide Blasen gleich sind. Es wird weiter angenommen, dass die Blasen eine
sphärische Form behalten mit Radien 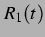 und
und 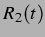 , wobei unterstellt wird, dass die
Blasen nicht zu dicht bei einer Grenzfläche oder beieinander liegen, und dass
keine Oberflächenmoden angeregt werden. Das Koordinatensystem werde so
gewählt, dass die erste Blase in seinem Ursprung sitzt
(s. Abbildung 2.2).
, wobei unterstellt wird, dass die
Blasen nicht zu dicht bei einer Grenzfläche oder beieinander liegen, und dass
keine Oberflächenmoden angeregt werden. Das Koordinatensystem werde so
gewählt, dass die erste Blase in seinem Ursprung sitzt
(s. Abbildung 2.2).
Abbildung 2.2: Koordinatensystem für das angenommene
Modell. Die erste Blase sitzt im Ursprung, die zweite im Abstand 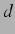 .
. 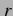 bezeichne die Radialkomponente und
bezeichne die Radialkomponente und
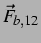 die sekundäre Bjerkneskraft von der ersten auf die
zweite Blase
die sekundäre Bjerkneskraft von der ersten auf die
zweite Blase
|
|
In [25] wurde die Flüssigkeit in der
Nähe der Blasen als inkompressibel angenommen. Dies gilt nun nicht mehr, da hier
eine endliche Schallgeschwindigkeit angenommen wird. Da diese jedoch bis auf eine
sehr kurze Phase beim Blasenkollaps groß gegen die Geschwindigkeit der
Blasenwand ist ([5]), ist die Machzahl
klein, wobei 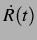 Ableitung des Blasenradius nach der Zeit, und
Ableitung des Blasenradius nach der Zeit, und 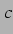 die
Schallgeschwindigkeit in Medium, also Wasser, bezeichne. Laut TRITTON
gilt eine inkompressible Näherung ([36]):
die
Schallgeschwindigkeit in Medium, also Wasser, bezeichne. Laut TRITTON
gilt eine inkompressible Näherung ([36]):
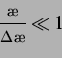 |
(2) |
(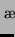 bezeichne die Dichte und
bezeichne die Dichte und 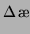 die Dichteänderung) für die Bewegungs-
Navier-Stokes-Gleichung, wenn
die Dichteänderung) für die Bewegungs-
Navier-Stokes-Gleichung, wenn
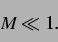 |
(3) |
Diese Bedingung ist bei den gegebenen Parametern erfüllt, solange für den
Anregungsdruck 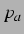 gilt:
gilt:
denn:
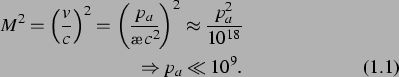
Dies ist für den Anregungsdruck und den gestreuten Druck erfüllt
(außer eventuell kurz nach einem heftigen Blasenkollaps). Durch Wegfallen der
Ableitungen nach den Winkeln (Radialsymmetrie wurde angenommen) erhält man dann
aus der Kontinuitätsgleichung in Kugelkoordinaten für die Radialkomponente
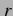 des
obigem Koordinatensystems das Geschwindigkeitsfeld
des
obigem Koordinatensystems das Geschwindigkeitsfeld 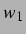 , das die Geschwindigkeit der
Flüssigkeitsteilchen am Ort der zweiten Blase, durch die Schwingung der ersten
Blase erzeugt, bestimmt:
, das die Geschwindigkeit der
Flüssigkeitsteilchen am Ort der zweiten Blase, durch die Schwingung der ersten
Blase erzeugt, bestimmt:
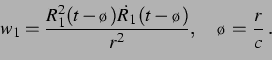
|
(4) |
Die Verzögerung um 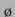 rührt von der Zeit, die der Druck für die
Strecke zwischen den beiden Blasen benötigt.
rührt von der Zeit, die der Druck für die
Strecke zwischen den beiden Blasen benötigt.
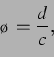 |
(5) |
wenn 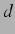 der Abstand der Blasen ist. Im Folgenden wird für
der Abstand der Blasen ist. Im Folgenden wird für 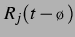 häufig auch
häufig auch 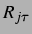 als synonyme Bezeichnung verwendet. Aus der Navier-Stokes-Gleichung erhält man
entsprechend das Druckfeld, das von der ersten Blase in die Flüssigkeit
abgegeben wird, bis auf Terme der Ordnung
als synonyme Bezeichnung verwendet. Aus der Navier-Stokes-Gleichung erhält man
entsprechend das Druckfeld, das von der ersten Blase in die Flüssigkeit
abgegeben wird, bis auf Terme der Ordnung 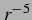 . Es gilt:
. Es gilt:
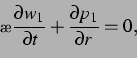
|
(6) |
und mit Gleichung (2.5) folgt nun
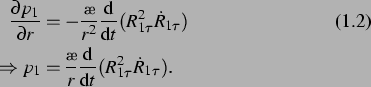
Das Druckfeld der ersten Blase wirkt zusätzlich zum Anregungsdruck auf die
zweite Blase (natürlich auch das der zweiten auf die erste). Sei
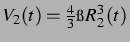 das Volumen der zweiten Blase und
das Volumen der zweiten Blase und
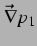 der Druckgradient, der an ihrer Position durch die erste Blase
erzeugt wird; dann ist
der Druckgradient, der an ihrer Position durch die erste Blase
erzeugt wird; dann ist
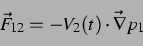
|
(7) |
die Kraft, die auf die zweite Blase wirkt. Somit erhält man für die auf die
zweite Blase in der Entfernung 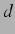 von der ersten wirkende Kraft:
von der ersten wirkende Kraft:
Dabei sind
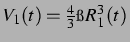 das Volumen der ersten Blase und
das Volumen der ersten Blase und 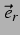 der radiale
Einheitsvektor.
der radiale
Einheitsvektor.
Mittelt man nun diese Kraft über eine Anregungsperiode durch partielle
Integration, erhält man die effektive Kraft auf die zweite Blase: die
sekundäre Bjerkneskraft:
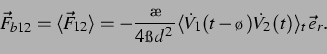
|
(9) |
Im Fall kleiner, linearer Schwingungen beider Blasen mit Amplituden 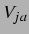 um das
Volumen der ruhenden Blase
um das
Volumen der ruhenden Blase
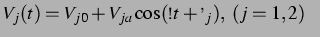 erhält man
für ein inkompressibles Fluid (also ohne Delay; s. [30]):
erhält man
für ein inkompressibles Fluid (also ohne Delay; s. [30]):
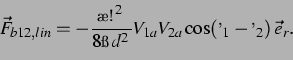
|
(10) |
Somit ist die Aussage der linearen Näherung ohne Delay, dass sich Blasenpaare
anziehen, die beide größer oder aber beide kleiner als der lineare
Resonanzradius sind, während sich gemischte Blasenpaare abstoßen
(hierzu später mehr). Es ist ersichtlich, dass die sekundäre Bjerkneskraft
für den Fall nicht delay-gekoppelter Blasen invariant gegen Indexvertauschung
 in Gleichung (2.11)
ist, da dann
in Gleichung (2.11)
ist, da dann 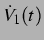 und
und 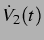 zum gleichen Zeitpunkt eingehen. Es ist zu
beachten, dass bei einem Wechsel der Indizes auch das Koordinatensystem wechselt, so
dass folgt: Bei instantan wechselwirkenden Blasen sind die sekundären
Bjerkneskräfte gleich groß und entgegengesetzt:
zum gleichen Zeitpunkt eingehen. Es ist zu
beachten, dass bei einem Wechsel der Indizes auch das Koordinatensystem wechselt, so
dass folgt: Bei instantan wechselwirkenden Blasen sind die sekundären
Bjerkneskräfte gleich groß und entgegengesetzt:
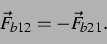 |
(11) |
Die Einführung des Delays wird diese Symmetrie auflösen, wie in
Kapitel 3 gezeigt wird.
Genaugenommen hängt die Delayzeit 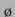 auch von den momentanen Blasenradien
auch von den momentanen Blasenradien 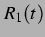 und
und
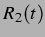 ([11]) ab. Außerdem verändert
sich
([11]) ab. Außerdem verändert
sich 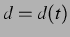 , falls die Blasen sich relativ zueinander bewegen. Falls sich die Blasen
relativ zur Flüssigkeit bewegen, müssen evtl. verschiedene Delayzeiten
wegen des Dopplereffekts berücksichtigt werden. Alle genannten Effekte werden
jedoch vernachlässigt, so dass
, falls die Blasen sich relativ zueinander bewegen. Falls sich die Blasen
relativ zur Flüssigkeit bewegen, müssen evtl. verschiedene Delayzeiten
wegen des Dopplereffekts berücksichtigt werden. Alle genannten Effekte werden
jedoch vernachlässigt, so dass
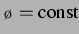 angenommen wird.
angenommen wird.




Nächste Seite: Keller-Miksis-Modell Aufwärts: Strukturbildung bei Kavitationsblasen Vorherige Seite:
Strukturbildung bei Kavitationsblasen
Inhalt
Stefan Kamphausen 2003-07-17
![\includegraphics [width=7cm]{EPS/koosys.eps}](img86.png)
![\includegraphics [width=7cm]{EPS/koosys.eps}](img86.png)
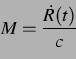
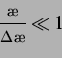
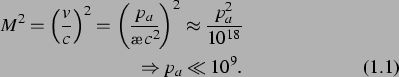
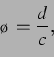
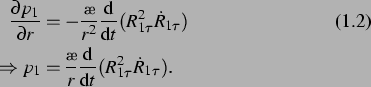
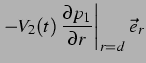
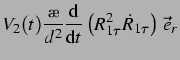
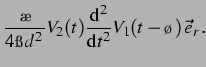
![]() um das
Volumen der ruhenden Blase
um das
Volumen der ruhenden Blase
![]() erhält man
für ein inkompressibles Fluid (also ohne Delay; s. [30]):
erhält man
für ein inkompressibles Fluid (also ohne Delay; s. [30]):![]() auch von den momentanen Blasenradien
auch von den momentanen Blasenradien ![]() und
und
![]() ([11]) ab. Außerdem verändert
sich
([11]) ab. Außerdem verändert
sich ![]() , falls die Blasen sich relativ zueinander bewegen. Falls sich die Blasen
relativ zur Flüssigkeit bewegen, müssen evtl. verschiedene Delayzeiten
wegen des Dopplereffekts berücksichtigt werden. Alle genannten Effekte werden
jedoch vernachlässigt, so dass
, falls die Blasen sich relativ zueinander bewegen. Falls sich die Blasen
relativ zur Flüssigkeit bewegen, müssen evtl. verschiedene Delayzeiten
wegen des Dopplereffekts berücksichtigt werden. Alle genannten Effekte werden
jedoch vernachlässigt, so dass
![]() angenommen wird.
angenommen wird.