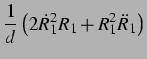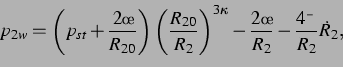Nächste Seite: Die linearisierte
Keller-Miksis-Gleichung Aufwärts: Strukturbildung bei Kavitationsblasen Vorherige Seite: Die sekundäre Bjerkneskraft
Inhalt
Keller-Miksis-Modell
Ausgehend von der in [29] verwendeten
Gleichung für die Dynamik der zweiten von zwei gekoppelten Kavitationsblasen,
mit
die ihrerseits vom Keller-Miksis-Modell stammt ([18], [29]),
erhält man die Gleichung für diese Blase im delay-gekoppelten Fall zu
Die Größen in der Reihenfolge ihres Auftretens sind in Tabelle 2.1 aufgelistet. Die dort angegebenen Parameter
orientieren sich am zitierten Kavitationsexperiment in Wasser bei einer 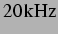 Schallanregung.
Schallanregung.
Tabelle 2.1: Verwendete Symbole, ihre Bedeutung und soweit
konstant ihre Werte in dieser Arbeit. Es wurden Normalbedingungen für
Wasser und Luftdruck angenommen (die Schallgeschwindigkeit wurde dabei etwas
aufgerundet).
| Symbol |
physikalische Größe |
Wert (falls konstant) |
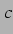 |
Schallgeschwindigkeit in Wasser |
 |
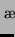 |
Dichte von Wasser |
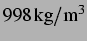 |
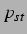 |
Umgebungsdruck |
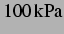 |
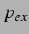 |
anregender Druck |
variabel |
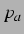 |
Amplitude der Anregung, falls kosinusförmig |
variabel |
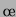 |
Oberflächenspannung |
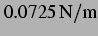 |
 |
Adiabatenexponent |
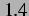 |
 |
Viskosität von Wasser |
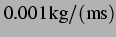 |
 |
Frequenz der Anregung |
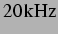 |
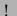 |
Kreisfrequenz der Anregung |
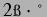 |
|
Durch Einsetzen von 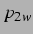 und Durchführen der Ableitung erhält man dann
für die kosinusförmige Anregung
und Durchführen der Ableitung erhält man dann
für die kosinusförmige Anregung
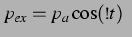
für die erste Blase für die zweite:
Durch Umstellen und Zusammenfassen erhält man eine weniger aufwendige Form
(speziell in Hinsicht auf die Numerik [29]):
für die erste Blase und entsprechend für die zweite:
Dieses System zweier nichtlinearer, delay-gekoppelter Differentialgleichungen wird
in Kapitel 4 untersucht werden, um aus der so
gewonnenen Kavitationsblasendynamik die sekundäre Bjerkneskraft zu
berechnen.




Nächste Seite: Die linearisierte
Keller-Miksis-Gleichung Aufwärts: Strukturbildung bei Kavitationsblasen Vorherige Seite: Die sekundäre Bjerkneskraft
Inhalt
Stefan Kamphausen 2003-07-17
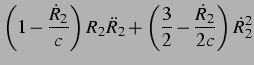
![$\displaystyle \frac{1}{\rho}\left(1+\frac{\dot{R}_2}{c}\right) \left[p_{2w}-p_{st}-p_{ex}\right]$](img126.png)
![$\displaystyle \frac{R_2}{\rho c} \ddt\left[p_{2w} - p_{ex}\right]$](img128.png)