



Nächste Seite: Die linearisierte
Keller-Miksis-Gleichung mit Aufwärts: Die linearisierte Keller-Miksis-Gleichung ohne Vorherige
Seite: Theorie Inhalt
Ergebnisse
Es wird ein Anregungsdruck von  betrachtet, bei dem die lineare Näherung
über weite Strecken noch gut gerechtfertigt sein sollte. Dieser Wert ist aber
bereits ein Grenzfall, wie in Abschnitt 5
gezeigt wird. Bei sehr kleinem Delay (Abbildung 3.1) ist die Bjerkneskraft nach dem linearisierten,
ungekoppelten Modell,
betrachtet, bei dem die lineare Näherung
über weite Strecken noch gut gerechtfertigt sein sollte. Dieser Wert ist aber
bereits ein Grenzfall, wie in Abschnitt 5
gezeigt wird. Bei sehr kleinem Delay (Abbildung 3.1) ist die Bjerkneskraft nach dem linearisierten,
ungekoppelten Modell, 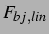 , für den Fall, dass beide Blasen entweder
kleiner oder größer als ihr Resonanzradius sind, anziehend. Umgekehrt
stoßen sie sich ab, wenn eine kleiner, die andere aber größer ist.
Das ist das Verhalten, das man von ungekoppelten linear schwingenden Blasen erwartet.
Das Delay hat hier also keinen nennenswerten Einfluss auf das Vorzeichen der
sekundären Bjerkneskraft. Außer in direkter Nähe der linearen
Resonanz lassen sich Die Indizes der Blasen austauschen, die Kraft der zweiten Blase
auf die erste ist gerade entgegengesetzt gleich der ersten auf die zweite.
, für den Fall, dass beide Blasen entweder
kleiner oder größer als ihr Resonanzradius sind, anziehend. Umgekehrt
stoßen sie sich ab, wenn eine kleiner, die andere aber größer ist.
Das ist das Verhalten, das man von ungekoppelten linear schwingenden Blasen erwartet.
Das Delay hat hier also keinen nennenswerten Einfluss auf das Vorzeichen der
sekundären Bjerkneskraft. Außer in direkter Nähe der linearen
Resonanz lassen sich Die Indizes der Blasen austauschen, die Kraft der zweiten Blase
auf die erste ist gerade entgegengesetzt gleich der ersten auf die zweite.
Abbildung: Links: sekundäre Bjerkneskräfte
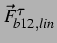 in der
in der 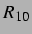 -
-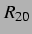 -Ebene für das
linearisierte Modell ohne Kopplung bei
-Ebene für das
linearisierte Modell ohne Kopplung bei  , entspricht einem
Blasenabstand von
, entspricht einem
Blasenabstand von
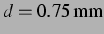 . Anregung dabei: Druck
. Anregung dabei: Druck
 und Frequenz
und Frequenz
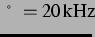 . Rechts: Das Vorzeichen der Bjerkneskräfte. Schwarz
bedeutet anziehende, weiß abstoßende Kräfte der ersten auf die
zweite Blase. Das Ergebnis stimmt mit der bekannten linearen Theorie
überein: sind beide Blasen kleiner oder größer als ihr linearer
Resonanzradius, ziehen sie sich an, sonst stoßen sie sich ab.
. Rechts: Das Vorzeichen der Bjerkneskräfte. Schwarz
bedeutet anziehende, weiß abstoßende Kräfte der ersten auf die
zweite Blase. Das Ergebnis stimmt mit der bekannten linearen Theorie
überein: sind beide Blasen kleiner oder größer als ihr linearer
Resonanzradius, ziehen sie sich an, sonst stoßen sie sich ab.
|
|
In den folgenden Abbildungen 3.2
bis 3.8 wird das Delay bei einem weiterhin
konstanten Anregungsdruck von
 von
von  (noch klein) auf
(noch klein) auf 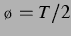 (Maximalwert)
erhöht. Der Betrag der Bjerkneskraft nimmt mit zunehmendem Abstand immer weiter
ab bis zu wenigen
(Maximalwert)
erhöht. Der Betrag der Bjerkneskraft nimmt mit zunehmendem Abstand immer weiter
ab bis zu wenigen 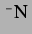 bei
bei 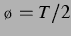 . Das ist auch zu erwarten, da die
Kraft ja in Gleichung (3.17) mit
. Das ist auch zu erwarten, da die
Kraft ja in Gleichung (3.17) mit 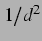 skaliert und
skaliert und 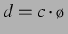 gilt.. Zu beachten ist bei all diesen Abbildungen, dass die
Extrema in den Abbildungen nicht notwendig die absoluten Extremwerte der
sekundären Bjerkneskraft sind, denn die Werte wurden auf einem festen Raster
bestimmt, so dass es nicht gewährleistet ist, Minima oder Maxima exakt zu
treffen, die sich aber auch nicht immens von den angezeigten unterscheiden
sollten
gilt.. Zu beachten ist bei all diesen Abbildungen, dass die
Extrema in den Abbildungen nicht notwendig die absoluten Extremwerte der
sekundären Bjerkneskraft sind, denn die Werte wurden auf einem festen Raster
bestimmt, so dass es nicht gewährleistet ist, Minima oder Maxima exakt zu
treffen, die sich aber auch nicht immens von den angezeigten unterscheiden
sollten
Abbildung 3.2: Sekundäre Bjerkneskraft und Vorzeichen wie
in Abbildung 3.1 bei  ,
entspricht einem Blasenabstand von
,
entspricht einem Blasenabstand von
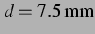 . In der Mitte wird der beginnende Symmetriebruch
sichtbar.
. In der Mitte wird der beginnende Symmetriebruch
sichtbar.
|
|
In Abbildung 3.2 ist bei  gegenüber Abbildung 3.1 noch kein
großer Unterschied bezüglich der Vorzeichen zu erkennen. Der Betrag der
Kräfte hat bedeutend abgenommen, das Schachbrettmuster der Vorzeichenverteilung
hat sich kaum geändert. Lediglich am Berührungspunkt aller Felder in der
Mitte kann man erkennen, dass sich die abstoßenden Bereiche etwas voneinander
entfernt haben. Dieser erkennbare Symmetriebruch rührt vom größeren
Delay. In Gleichung (3.17) stehen im
Argument des Kosinus nicht mehr nur die Phasenwinkel der Blasenschwingungen zur
Anregung, sondern zusätzlich noch eine weitere Phase durch das Delay. Somit
lassen sich die Indizes in dieser Gleichung nicht mehr ohne weiteres vertauschen. Die
Symmetrie wird sichtbar gebrochen, sobald
gegenüber Abbildung 3.1 noch kein
großer Unterschied bezüglich der Vorzeichen zu erkennen. Der Betrag der
Kräfte hat bedeutend abgenommen, das Schachbrettmuster der Vorzeichenverteilung
hat sich kaum geändert. Lediglich am Berührungspunkt aller Felder in der
Mitte kann man erkennen, dass sich die abstoßenden Bereiche etwas voneinander
entfernt haben. Dieser erkennbare Symmetriebruch rührt vom größeren
Delay. In Gleichung (3.17) stehen im
Argument des Kosinus nicht mehr nur die Phasenwinkel der Blasenschwingungen zur
Anregung, sondern zusätzlich noch eine weitere Phase durch das Delay. Somit
lassen sich die Indizes in dieser Gleichung nicht mehr ohne weiteres vertauschen. Die
Symmetrie wird sichtbar gebrochen, sobald  groß genug ist, dass es im Argument
eine Rolle spielt und nicht mehr gilt
groß genug ist, dass es im Argument
eine Rolle spielt und nicht mehr gilt
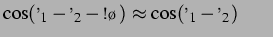 .
.
Abbildung: Sekundäre Bjerkneskraft und Vorzeichen wie in
Abbildung 3.1 bei 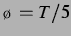 ,
entspricht einem Blasenabstand von
,
entspricht einem Blasenabstand von
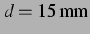 . Die abstoßenden Bereiche entfernen sich
zunächst langsam voneinander.
. Die abstoßenden Bereiche entfernen sich
zunächst langsam voneinander.
|
|
Dieser Trend setzt sich in Abbildung 3.3
weiter fort. Doch trotz der recht großen Änderung in 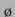 von
von 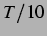 auf
auf 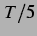 , also
einer Verdopplung des Blasenabstandes von
, also
einer Verdopplung des Blasenabstandes von
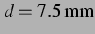 auf
auf 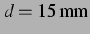 , ist die Änderung im Vorzeichenbild noch
sehr gering. Im Bereich um
, ist die Änderung im Vorzeichenbild noch
sehr gering. Im Bereich um  ändert es sich hingegen sehr schnell.
Abbildung 3.4 zeigt bei
ändert es sich hingegen sehr schnell.
Abbildung 3.4 zeigt bei 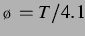 die
Tendenz der Änderungen deutlich: der linke obere abstoßende Bereich, wenn
die erste Blase kleiner als ihr Resonanzradius, die zweite hingegen größer
ist, zieht sich immer weiter zurück, während sich der untere Bereich
für die entsprechend umgedrehten Resonanzradiusverhältnisse aufweitet. Die
ursprüngliche Symmetrie ist hier schon kaum noch zu erkennen.
die
Tendenz der Änderungen deutlich: der linke obere abstoßende Bereich, wenn
die erste Blase kleiner als ihr Resonanzradius, die zweite hingegen größer
ist, zieht sich immer weiter zurück, während sich der untere Bereich
für die entsprechend umgedrehten Resonanzradiusverhältnisse aufweitet. Die
ursprüngliche Symmetrie ist hier schon kaum noch zu erkennen.
Abbildung 3.4: Sekundäre Bjerkneskraft und Vorzeichen wie
in Abbildung 3.1 bei 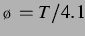 ,
entspricht einem Blasenabstand von
,
entspricht einem Blasenabstand von
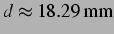 . Im Bereich um
. Im Bereich um  ändern sich die
Vorzeichen sehr schnell.
ändern sich die
Vorzeichen sehr schnell.
|
|
Abbildung: Sekundäre Bjerkneskraft und Vorzeichen wie in
Abbildung 3.1 bei  ,
entspricht einem Blasenabstand von
,
entspricht einem Blasenabstand von
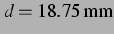 . Eine große Blase
. Eine große Blase
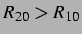 wird von der kleinen angezogen. Eine kleine Blase wird
von der großen jedoch abgestoßen.
wird von der kleinen angezogen. Eine kleine Blase wird
von der großen jedoch abgestoßen.
|
|
In Abbildung 3.5 schließlich ist
bei  der linke, obere anziehende Bereich ganz aus dem dargestellten
Ausschnitt der
der linke, obere anziehende Bereich ganz aus dem dargestellten
Ausschnitt der 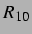 -
-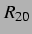 -Ebene verschwunden und der rechte, untere abstoßende Bereich so
gewachsen, dass die
-Ebene verschwunden und der rechte, untere abstoßende Bereich so
gewachsen, dass die 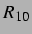 -
-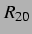 -Ebene durch die Winkelhalbierende geteilt wird. Damit ist
die sekundäre Bjerkneskraft anziehend, wenn die 2. Blase einen
größeren Ruheradius hat als die erste. Da hier ja die Kraft der ersten auf
die zweite Blase dargestellt wird, lässt sich dieses Ergebnis
folgendermaßen interpretieren: Eine große zweite Blase wird von einer
kleineren ersten Blase angezogen, während aber umgekehrt die kleinere erste
Blase von der großen zweiten abgestoßen wird. Somit ergibt sich die
Situation in Abbildung 3.6: Ohne weitere
äußere Kräfte wie die primäre Bjerkneskraft setzen sich die
Blasen nur aufgrund der sekundären Bjerkneskraft in dieselbe Richtung in
Bewegung. Ein solches Ergebnis ist bemerkenswert, da sich dieses Verhalten ohne Delay
bei den gemachten Annahmen nicht voraussagen lässt. In dem Fall gilt ja eine
Symmetrie bezüglich der Vertauschung der Indizes und somit stoßen sich die
Blasen immer gegenseitig ab oder aber ziehen sich gegenseitig an
[vgl. Gl. (2.13)]. Hier wirkt jedoch die
größere abstoßend und die kleinere anziehend, so dass sich auch in
jedem Fall der Schwerpunkt beider Blasen bewegt. Dieses widerspricht nicht der
Impuls- oder Energieerhaltung, da beides mit dem anregenden Schallfeld ausgetauscht
werden kann. Die relative Position der beiden Blasen zueinander kann sich
natürlich trotzdem verändern - das hängt von der absoluten
Größe der Bjerkneskräfte (primäre und sekundäre) sowie
Reibungs- und Trägheitskräften ab. Solche Blasenpaare lassen sich
übrigens immer finden, sobald die Austauschsymmetrie der Indizes (also der
Ruheradien) bezüglich des Vorzeichens verletzt ist, also im Prinzip bereits bei
-Ebene durch die Winkelhalbierende geteilt wird. Damit ist
die sekundäre Bjerkneskraft anziehend, wenn die 2. Blase einen
größeren Ruheradius hat als die erste. Da hier ja die Kraft der ersten auf
die zweite Blase dargestellt wird, lässt sich dieses Ergebnis
folgendermaßen interpretieren: Eine große zweite Blase wird von einer
kleineren ersten Blase angezogen, während aber umgekehrt die kleinere erste
Blase von der großen zweiten abgestoßen wird. Somit ergibt sich die
Situation in Abbildung 3.6: Ohne weitere
äußere Kräfte wie die primäre Bjerkneskraft setzen sich die
Blasen nur aufgrund der sekundären Bjerkneskraft in dieselbe Richtung in
Bewegung. Ein solches Ergebnis ist bemerkenswert, da sich dieses Verhalten ohne Delay
bei den gemachten Annahmen nicht voraussagen lässt. In dem Fall gilt ja eine
Symmetrie bezüglich der Vertauschung der Indizes und somit stoßen sich die
Blasen immer gegenseitig ab oder aber ziehen sich gegenseitig an
[vgl. Gl. (2.13)]. Hier wirkt jedoch die
größere abstoßend und die kleinere anziehend, so dass sich auch in
jedem Fall der Schwerpunkt beider Blasen bewegt. Dieses widerspricht nicht der
Impuls- oder Energieerhaltung, da beides mit dem anregenden Schallfeld ausgetauscht
werden kann. Die relative Position der beiden Blasen zueinander kann sich
natürlich trotzdem verändern - das hängt von der absoluten
Größe der Bjerkneskräfte (primäre und sekundäre) sowie
Reibungs- und Trägheitskräften ab. Solche Blasenpaare lassen sich
übrigens immer finden, sobald die Austauschsymmetrie der Indizes (also der
Ruheradien) bezüglich des Vorzeichens verletzt ist, also im Prinzip bereits bei
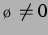 , in Abbildung 3.1. Bei
, in Abbildung 3.1. Bei
 ist die Symmetrie in diesem Sinne maximal gebrochen, da sich keine
Blasenpaare mehr gegenseitig abstoßen oder gegenseitig anziehen. Nur zwischen
gleichgroßen Blasen wirkt gar keine Kraft:
ist die Symmetrie in diesem Sinne maximal gebrochen, da sich keine
Blasenpaare mehr gegenseitig abstoßen oder gegenseitig anziehen. Nur zwischen
gleichgroßen Blasen wirkt gar keine Kraft:

Abbildung: Sekundäre Bjerkneskräfte bei  für zwei verschieden große Blasen. Sie zeigen in dieselbe Richtung.
für zwei verschieden große Blasen. Sie zeigen in dieselbe Richtung.
|
|
Wie aus der Gleichung (3.17) zu erwarten
ist (Verschiebung des Kosinus um seine halbe Periodenlänge), kehrt sich diese
Sequenz von  bis
bis 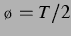 genau um, bis in Abbildung 3.8 das inverse Vorzeichenbild von Abbildung 3.1 zu sehen ist. Eine weitere Erhöhung des
Delays würde die Vorzeichenmuster aus den Abbildungen 3.1 bis 3.8
mit jeweils Schwarz und Weiß vertauscht hervorbringen.
genau um, bis in Abbildung 3.8 das inverse Vorzeichenbild von Abbildung 3.1 zu sehen ist. Eine weitere Erhöhung des
Delays würde die Vorzeichenmuster aus den Abbildungen 3.1 bis 3.8
mit jeweils Schwarz und Weiß vertauscht hervorbringen.
Die Einführung eines Delays lässt bereits bei einer Linearisierung des
Keller-Miksis-Modells und ohne eine gegenseitige Kopplung der Blasen eine neue
Aussage zu, die ohne das Delay nicht möglich ist: Ein Bruch der Symmetrie der
sekundären Bjerkneskraft in der 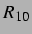 -
-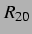 -Ebene, der in einer Kraft resultiert, die
zwei Blasen in eine Richtung bewegt. Dies tritt bei der betrachteten
Anregungsfrequenz jedoch erst bei sehr großem Blasenabstand auf, so dass der
Betrag dieser Kraft, der ja mit
-Ebene, der in einer Kraft resultiert, die
zwei Blasen in eine Richtung bewegt. Dies tritt bei der betrachteten
Anregungsfrequenz jedoch erst bei sehr großem Blasenabstand auf, so dass der
Betrag dieser Kraft, der ja mit 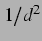 abfällt, nicht sehr groß ist und ihr
Einfluss unter Umständen nicht sehr relevant für die Dynamik ist.
abfällt, nicht sehr groß ist und ihr
Einfluss unter Umständen nicht sehr relevant für die Dynamik ist.
Abbildung 3.7: Bjerkneskraft und Vorzeichen wie in
Abbildung 3.1 bei 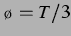 ,
entspricht einem Blasenabstand von
,
entspricht einem Blasenabstand von
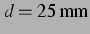 .
.
|
|
Abbildung 3.8: Bjerkneskraft und Vorzeichen wie in
Abbildung 3.1 bei 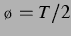 ,
entspricht einem Blasenabstand von
,
entspricht einem Blasenabstand von
 . Inverses Vorzeichenbild gegenüber Abb. 3.1. Die gesamte Vorzeichenmusterfolge von
. Inverses Vorzeichenbild gegenüber Abb. 3.1. Die gesamte Vorzeichenmusterfolge von
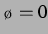 bis
bis  , von der hier die erste Hälfte gezeigt wurde,
da die zweite Hälfte das entsprechende Verhalten mit umgedrehten
Vorzeichen zeigt, wiederholt sich für höhere
, von der hier die erste Hälfte gezeigt wurde,
da die zweite Hälfte das entsprechende Verhalten mit umgedrehten
Vorzeichen zeigt, wiederholt sich für höhere 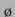 mit der
Periodenlänge
mit der
Periodenlänge 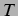 .
.
|
|




Nächste Seite: Die linearisierte
Keller-Miksis-Gleichung mit Aufwärts: Die linearisierte Keller-Miksis-Gleichung ohne Vorherige
Seite: Theorie Inhalt
Stefan Kamphausen 2003-07-17
![\includegraphics [width=8.5cm]{Linear/nokopp_100.ps}](img240.png)
![\includegraphics [width=6.791cm]{Linear/nokopp_100_sig.ps}](img241.png)
![\includegraphics [width=8.5cm]{Linear/nokopp_100.ps}](img240.png)
![\includegraphics [width=6.791cm]{Linear/nokopp_100_sig.ps}](img241.png)
![]() von
von ![]() (noch klein) auf
(noch klein) auf ![]() (Maximalwert)
erhöht. Der Betrag der Bjerkneskraft nimmt mit zunehmendem Abstand immer weiter
ab bis zu wenigen
(Maximalwert)
erhöht. Der Betrag der Bjerkneskraft nimmt mit zunehmendem Abstand immer weiter
ab bis zu wenigen ![]() bei
bei ![]() . Das ist auch zu erwarten, da die
Kraft ja in Gleichung (3.17) mit
. Das ist auch zu erwarten, da die
Kraft ja in Gleichung (3.17) mit ![]() skaliert und
skaliert und ![]() gilt.. Zu beachten ist bei all diesen Abbildungen, dass die
Extrema in den Abbildungen nicht notwendig die absoluten Extremwerte der
sekundären Bjerkneskraft sind, denn die Werte wurden auf einem festen Raster
bestimmt, so dass es nicht gewährleistet ist, Minima oder Maxima exakt zu
treffen, die sich aber auch nicht immens von den angezeigten unterscheiden
sollten
gilt.. Zu beachten ist bei all diesen Abbildungen, dass die
Extrema in den Abbildungen nicht notwendig die absoluten Extremwerte der
sekundären Bjerkneskraft sind, denn die Werte wurden auf einem festen Raster
bestimmt, so dass es nicht gewährleistet ist, Minima oder Maxima exakt zu
treffen, die sich aber auch nicht immens von den angezeigten unterscheiden
sollten![\includegraphics [width=8.5cm]{Linear/nokopp_10.ps}](img248.png)
![\includegraphics [width=6.791cm]{Linear/nokopp_10_sig.ps}](img249.png)
![\includegraphics [width=8.5cm]{Linear/nokopp_5.ps}](img252.png)
![\includegraphics [width=6.791cm]{Linear/nokopp_5_sig.ps}](img253.png)
![\includegraphics [width=8.5cm]{Linear/nokopp_4.1.ps}](img257.png)
![\includegraphics [width=6.791cm]{Linear/nokopp_4.1_sig.ps}](img258.png)
![\includegraphics [width=8.5cm]{Linear/nokopp_4.ps}](img260.png)
![\includegraphics [width=6.791cm]{Linear/nokopp_4_sig.ps}](img261.png)
![]() der linke, obere anziehende Bereich ganz aus dem dargestellten
Ausschnitt der
der linke, obere anziehende Bereich ganz aus dem dargestellten
Ausschnitt der ![]() -
-![]() -Ebene verschwunden und der rechte, untere abstoßende Bereich so
gewachsen, dass die
-Ebene verschwunden und der rechte, untere abstoßende Bereich so
gewachsen, dass die ![]() -
-![]() -Ebene durch die Winkelhalbierende geteilt wird. Damit ist
die sekundäre Bjerkneskraft anziehend, wenn die 2. Blase einen
größeren Ruheradius hat als die erste. Da hier ja die Kraft der ersten auf
die zweite Blase dargestellt wird, lässt sich dieses Ergebnis
folgendermaßen interpretieren: Eine große zweite Blase wird von einer
kleineren ersten Blase angezogen, während aber umgekehrt die kleinere erste
Blase von der großen zweiten abgestoßen wird. Somit ergibt sich die
Situation in Abbildung 3.6: Ohne weitere
äußere Kräfte wie die primäre Bjerkneskraft setzen sich die
Blasen nur aufgrund der sekundären Bjerkneskraft in dieselbe Richtung in
Bewegung. Ein solches Ergebnis ist bemerkenswert, da sich dieses Verhalten ohne Delay
bei den gemachten Annahmen nicht voraussagen lässt. In dem Fall gilt ja eine
Symmetrie bezüglich der Vertauschung der Indizes und somit stoßen sich die
Blasen immer gegenseitig ab oder aber ziehen sich gegenseitig an
[vgl. Gl. (2.13)]. Hier wirkt jedoch die
größere abstoßend und die kleinere anziehend, so dass sich auch in
jedem Fall der Schwerpunkt beider Blasen bewegt. Dieses widerspricht nicht der
Impuls- oder Energieerhaltung, da beides mit dem anregenden Schallfeld ausgetauscht
werden kann. Die relative Position der beiden Blasen zueinander kann sich
natürlich trotzdem verändern - das hängt von der absoluten
Größe der Bjerkneskräfte (primäre und sekundäre) sowie
Reibungs- und Trägheitskräften ab. Solche Blasenpaare lassen sich
übrigens immer finden, sobald die Austauschsymmetrie der Indizes (also der
Ruheradien) bezüglich des Vorzeichens verletzt ist, also im Prinzip bereits bei
-Ebene durch die Winkelhalbierende geteilt wird. Damit ist
die sekundäre Bjerkneskraft anziehend, wenn die 2. Blase einen
größeren Ruheradius hat als die erste. Da hier ja die Kraft der ersten auf
die zweite Blase dargestellt wird, lässt sich dieses Ergebnis
folgendermaßen interpretieren: Eine große zweite Blase wird von einer
kleineren ersten Blase angezogen, während aber umgekehrt die kleinere erste
Blase von der großen zweiten abgestoßen wird. Somit ergibt sich die
Situation in Abbildung 3.6: Ohne weitere
äußere Kräfte wie die primäre Bjerkneskraft setzen sich die
Blasen nur aufgrund der sekundären Bjerkneskraft in dieselbe Richtung in
Bewegung. Ein solches Ergebnis ist bemerkenswert, da sich dieses Verhalten ohne Delay
bei den gemachten Annahmen nicht voraussagen lässt. In dem Fall gilt ja eine
Symmetrie bezüglich der Vertauschung der Indizes und somit stoßen sich die
Blasen immer gegenseitig ab oder aber ziehen sich gegenseitig an
[vgl. Gl. (2.13)]. Hier wirkt jedoch die
größere abstoßend und die kleinere anziehend, so dass sich auch in
jedem Fall der Schwerpunkt beider Blasen bewegt. Dieses widerspricht nicht der
Impuls- oder Energieerhaltung, da beides mit dem anregenden Schallfeld ausgetauscht
werden kann. Die relative Position der beiden Blasen zueinander kann sich
natürlich trotzdem verändern - das hängt von der absoluten
Größe der Bjerkneskräfte (primäre und sekundäre) sowie
Reibungs- und Trägheitskräften ab. Solche Blasenpaare lassen sich
übrigens immer finden, sobald die Austauschsymmetrie der Indizes (also der
Ruheradien) bezüglich des Vorzeichens verletzt ist, also im Prinzip bereits bei
![]() , in Abbildung 3.1. Bei
, in Abbildung 3.1. Bei
![]() ist die Symmetrie in diesem Sinne maximal gebrochen, da sich keine
Blasenpaare mehr gegenseitig abstoßen oder gegenseitig anziehen. Nur zwischen
gleichgroßen Blasen wirkt gar keine Kraft:
ist die Symmetrie in diesem Sinne maximal gebrochen, da sich keine
Blasenpaare mehr gegenseitig abstoßen oder gegenseitig anziehen. Nur zwischen
gleichgroßen Blasen wirkt gar keine Kraft:
![\includegraphics [width=4cm]{EPS/running_bubs.eps}](img265.png)
![]() bis
bis ![]() genau um, bis in Abbildung 3.8 das inverse Vorzeichenbild von Abbildung 3.1 zu sehen ist. Eine weitere Erhöhung des
Delays würde die Vorzeichenmuster aus den Abbildungen 3.1 bis 3.8
mit jeweils Schwarz und Weiß vertauscht hervorbringen.
genau um, bis in Abbildung 3.8 das inverse Vorzeichenbild von Abbildung 3.1 zu sehen ist. Eine weitere Erhöhung des
Delays würde die Vorzeichenmuster aus den Abbildungen 3.1 bis 3.8
mit jeweils Schwarz und Weiß vertauscht hervorbringen.![]() -
-![]() -Ebene, der in einer Kraft resultiert, die
zwei Blasen in eine Richtung bewegt. Dies tritt bei der betrachteten
Anregungsfrequenz jedoch erst bei sehr großem Blasenabstand auf, so dass der
Betrag dieser Kraft, der ja mit
-Ebene, der in einer Kraft resultiert, die
zwei Blasen in eine Richtung bewegt. Dies tritt bei der betrachteten
Anregungsfrequenz jedoch erst bei sehr großem Blasenabstand auf, so dass der
Betrag dieser Kraft, der ja mit ![]() abfällt, nicht sehr groß ist und ihr
Einfluss unter Umständen nicht sehr relevant für die Dynamik ist.
abfällt, nicht sehr groß ist und ihr
Einfluss unter Umständen nicht sehr relevant für die Dynamik ist.![\includegraphics [width=8.5cm]{Linear/nokopp_3.ps}](img266.png)
![\includegraphics [width=6.791cm]{Linear/nokopp_3_sig.ps}](img267.png)
![\includegraphics [width=8.5cm]{Linear/nokopp_2.ps}](img269.png)
![\includegraphics [width=6.791cm]{Linear/nokopp_2_sig.ps}](img270.png)