



Nächste Seite: Theorie
Aufwärts: Die linearisierte
Keller-Miksis-Gleichung Vorherige Seite: Ergebnisse Inhalt
Die linearisierte Keller-Miksis-Gleichung mit Kopplung
Es soll nun in der linearisierten Keller-Miksis-Gleichung ein Kopplungsterm
eingeführt werden, der den Einfluss durch den abgestrahlten Schalldruck der
einen Blase auf die Dynamik der anderen in die Bewegungsgleichung einbezieht. Dieser
zusätzliche Beitrag zur Anregung einer Blase skaliert mit 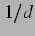 , nimmt also
ebenfalls (wie auch die sekundäre Bjerkneskraft) mit zunehmendem Abstand ab. Es
wird erwartet, dass auch hier die Symmetrie des instantan gekoppelten Modells aus [25] gebrochen wird. Erneut wird eine kleine
Schwingung der Blasen um ihren Ruheradius angenommen, so dass die Gleichung, die
für die sekundäre Bjerkneskraft bei harmonischen Blasenschwingungen
hergeleitet wurde (3.17), weiterhin gilt.
Aber es liegen nun keine einzelnen periodisch getriebenen, gedämpften
harmonischen Oszillatoren mehr vor, sondern zwei nichtlinear gekoppelte.
, nimmt also
ebenfalls (wie auch die sekundäre Bjerkneskraft) mit zunehmendem Abstand ab. Es
wird erwartet, dass auch hier die Symmetrie des instantan gekoppelten Modells aus [25] gebrochen wird. Erneut wird eine kleine
Schwingung der Blasen um ihren Ruheradius angenommen, so dass die Gleichung, die
für die sekundäre Bjerkneskraft bei harmonischen Blasenschwingungen
hergeleitet wurde (3.17), weiterhin gilt.
Aber es liegen nun keine einzelnen periodisch getriebenen, gedämpften
harmonischen Oszillatoren mehr vor, sondern zwei nichtlinear gekoppelte.
Unterabschnitte
Stefan Kamphausen 2003-07-17