



Nächste Seite: Ergebnisse der
numerischen Simulationen Aufwärts: Die linearisierte Keller-Miksis-Gleichung mit Vorherige
Seite: Theorie Inhalt
Ergebnisse
Zur Berechnung der sekundären Bjerkneskraft nach Formel (3.17) wurden 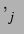 und
und 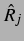 nach den
Gleichungen (3.26) und (3.27) bestimmt, und in den Abbildung 3.13 bis 3.20
wurde der Betrag der sekundären Bjerkneskraft nach dem linearisierten,
delay-gekoppelten Modell,
nach den
Gleichungen (3.26) und (3.27) bestimmt, und in den Abbildung 3.13 bis 3.20
wurde der Betrag der sekundären Bjerkneskraft nach dem linearisierten,
delay-gekoppelten Modell, 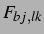 , aufgetragen. Der Anregungsdruck betrug wieder
, aufgetragen. Der Anregungsdruck betrug wieder
 und die Anregungsfrequenz
und die Anregungsfrequenz
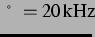 .
.
Abbildung: Links: sekundäre Bjerkneskraft für den
Fall gekoppelter Blasen bei harmonischer Schwingung und
 , entspricht
, entspricht
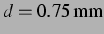 . Der anregende Schalldruck beträgt
. Der anregende Schalldruck beträgt
 . Rechts: Das Vorzeichen der sekundären
Bjerkneskraft. Die Ruheradien, bei denen der Vorzeichenwechsel stattfindet,
sind gegenüber dem nicht gekoppelten Fall erhöht
(vgl. Abb. 3.1). Die
Ruheradien, bei denen die sekundäre Bjerkneskraft sehr groß wird,
liegen weit außen in der dargestellten Ebene, was man durch Vergleich mit
der Abbildung 3.9 leicht versteht.
Man beachte die Einheit der Kraft:
. Rechts: Das Vorzeichen der sekundären
Bjerkneskraft. Die Ruheradien, bei denen der Vorzeichenwechsel stattfindet,
sind gegenüber dem nicht gekoppelten Fall erhöht
(vgl. Abb. 3.1). Die
Ruheradien, bei denen die sekundäre Bjerkneskraft sehr groß wird,
liegen weit außen in der dargestellten Ebene, was man durch Vergleich mit
der Abbildung 3.9 leicht versteht.
Man beachte die Einheit der Kraft: 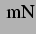 in dieser und der nächsten
Abbildung (3.14) statt
in dieser und der nächsten
Abbildung (3.14) statt 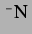 wie in allen anderen Abbildungen in diesem Abschnitt.
wie in allen anderen Abbildungen in diesem Abschnitt.
|
|
In Abbildung 3.13 fällt sofort auf,
dass sich die Ruheradien, bei denen in der sekundären Bjerkneskraft das
Vorzeichen wechselt, zu höheren Radien verschoben haben. Bei  liegen sie
bei bei etwa
liegen sie
bei bei etwa
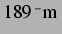 . Eine Diskussion hierzu findet sich später in diesem
Abschnitt. Da der Unterschied der Abbildungen 3.13 und 3.15
sehr groß ist, wurde noch ein weiterer Wert,
. Eine Diskussion hierzu findet sich später in diesem
Abschnitt. Da der Unterschied der Abbildungen 3.13 und 3.15
sehr groß ist, wurde noch ein weiterer Wert, 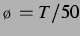 in die Serie mit aufgenommen,
um zu betrachten, wie sich die Bjerkneskraftlandschaft bei sehr kleinem Delay
verändert.
in die Serie mit aufgenommen,
um zu betrachten, wie sich die Bjerkneskraftlandschaft bei sehr kleinem Delay
verändert.
Abbildung: Sekundäre Bjerkneskraft für
delay-gekoppelt schwingende Blasen wie in Abbildung 3.13 sowie Vorzeichen bei 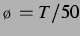 , entspricht
, entspricht
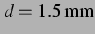 . Hierzu gibt es keine vergleichbare Abbildung im
ungekoppelten Fall, da sich dort zwischen
. Hierzu gibt es keine vergleichbare Abbildung im
ungekoppelten Fall, da sich dort zwischen  und
und 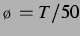 kaum
etwas ändert. Hier jedoch liegen die Vorzeichenwechsel durch die geringere
Kopplung bei doppeltem Abstand gegenüber Abbildung 3.13 wieder bei geringeren Ruheradien. Die
Resonanzkämme wachsen von außen heran.
kaum
etwas ändert. Hier jedoch liegen die Vorzeichenwechsel durch die geringere
Kopplung bei doppeltem Abstand gegenüber Abbildung 3.13 wieder bei geringeren Ruheradien. Die
Resonanzkämme wachsen von außen heran.
|
|
Abbildung 3.15: Sekundäre Bjerkneskraft für
delay-gekoppelt schwingende Blasen wie in Abbildung 3.13 sowie Vorzeichen bei  , entspricht
, entspricht
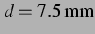 . Die Situation gleicht beinahe der des ungekoppelten
Falls aus Abbildung 3.2. Die
Vorzeichenwechsel liegen bei leicht höheren Ruheradien (etwa
. Die Situation gleicht beinahe der des ungekoppelten
Falls aus Abbildung 3.2. Die
Vorzeichenwechsel liegen bei leicht höheren Ruheradien (etwa
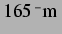 statt
statt
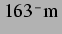 ). Man erkennt auch das Verhalten der Resonanzradien, das
in Abschnitt 3.2.1 betrachtet wurde,
wieder. Durch die abnehmende Kopplung nähern sich die Muster einem Kamm
beim Resonanzradius.
). Man erkennt auch das Verhalten der Resonanzradien, das
in Abschnitt 3.2.1 betrachtet wurde,
wieder. Durch die abnehmende Kopplung nähern sich die Muster einem Kamm
beim Resonanzradius.
|
|
Was in Abbildung 3.15 weiter gegenüber
Abbildung 3.2 auffällt ist, dass die
ausgezeichneten Flächen, die jeweils das gleiche Vorzeichen der sekundären
Bjerkneskraft anzeigen, noch nicht sichtbar auseinander gegangen sind. Dies wird auch
in den darauffolgenden Abbildungen jeweils im Vergleich zum entsprechenden Bild aus
Abschnitt 3.1.2 sichtbar. Das Intervall um
 , in dem die Symmetrie sich plötzlich verliert und die Gebiete
gleichen Vorzeichens sich schnell verlagern, ist kleiner geworden.
, in dem die Symmetrie sich plötzlich verliert und die Gebiete
gleichen Vorzeichens sich schnell verlagern, ist kleiner geworden.
Abbildung: Sekundäre Bjerkneskraft für
delay-gekoppelt schwingende Blasen wie in Abbildung 3.13 sowie Vorzeichen bei 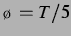 , entspricht
, entspricht
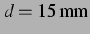 . Der Vergleich mit Abbildung 3.3 zeigt keinen Unterschied bei den
Vorzeichenwechseln, die Flächen sind jedoch noch nicht so weit auseinander
gedriftet. Die Kämme werden durch die größere Entfernung der
Blasen flacher. Der Betrag der Kraft unterscheidet sich nicht mehr wesentlich
vom ungekoppelten Fall.
. Der Vergleich mit Abbildung 3.3 zeigt keinen Unterschied bei den
Vorzeichenwechseln, die Flächen sind jedoch noch nicht so weit auseinander
gedriftet. Die Kämme werden durch die größere Entfernung der
Blasen flacher. Der Betrag der Kraft unterscheidet sich nicht mehr wesentlich
vom ungekoppelten Fall.
|
|
Die Bilder für 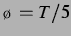 bis
bis 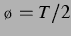 ähneln denen im Fall
ungekoppelter Blasen. Im Bereich um
ähneln denen im Fall
ungekoppelter Blasen. Im Bereich um  ändert sich das Vorzeichenmuster
sehr schnell und bei
ändert sich das Vorzeichenmuster
sehr schnell und bei 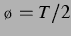 sind die Vorzeichen gerade umgedreht zu denen bei
sind die Vorzeichen gerade umgedreht zu denen bei
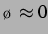 . Der Betrag der sekundären Bjerkneskraft ist bei sehr
kleinem Delay größer als bei ungekoppelt schwingenden Blasen, was sich
aber mit zunehmendem Abstand ändert. Der Vergleich mit den Abbildungen 3.9 bis 3.12 aus Abschnitt 3.2.1 erklärt die bereits angesprochene Verteilung
der Extremwerte der sekundären Bjerkneskraft. Dort wurde die Amplitude
. Der Betrag der sekundären Bjerkneskraft ist bei sehr
kleinem Delay größer als bei ungekoppelt schwingenden Blasen, was sich
aber mit zunehmendem Abstand ändert. Der Vergleich mit den Abbildungen 3.9 bis 3.12 aus Abschnitt 3.2.1 erklärt die bereits angesprochene Verteilung
der Extremwerte der sekundären Bjerkneskraft. Dort wurde die Amplitude 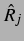 der
der 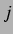 -ten Blase gezeigt, und es wurde festgestellt, dass dieses Muster durch die
abnehmende Kopplung an Komplexität verliert und sich zu einem einfachen Kamm am
Resonanzradius der jeweiligen Blase entwickelt. Dieses Verhalten bestimmt auch
wesentlich die sekundären Bjerkneskraft-Gebirge, bei denen sich ein
ähnliches Verhalten erkennen lässt. Während in der Abbildung 3.13 bei einem Delay von
-ten Blase gezeigt, und es wurde festgestellt, dass dieses Muster durch die
abnehmende Kopplung an Komplexität verliert und sich zu einem einfachen Kamm am
Resonanzradius der jeweiligen Blase entwickelt. Dieses Verhalten bestimmt auch
wesentlich die sekundären Bjerkneskraft-Gebirge, bei denen sich ein
ähnliches Verhalten erkennen lässt. Während in der Abbildung 3.13 bei einem Delay von  noch ein Muster
zu sehen ist, in dem die auffälligen Gebiete von dem Punkt, an dem beide Blasen
ihre Resonanzruheradien haben, entfernt sind, nähern sie sich für
abnehmende Kopplung diesem Punkt immer mehr an. Die Kämme der sekundären
Bjerkneskräfte bei den Resonanzradien werden immer deutlicher, bis sie durch die
große Entfernung der Blasen stark abgeschwächt werden. Ein Vergleich der
Abbildungen 3.13 bis 3.15 mit den Abbildungen 3.9 bis 3.11
zeigt eine deutliche Ähnlichkeit. Zunächst liegen die hohen Berge der
Amplituden- Bjerkneskraft-Gebirge weit außen in der betrachteten Ebene, dann
wandern diese Gipfel zum zentralen Punkt, an dem beide Blasen ihren
Resonanzruheradius haben, und von außen wächst ein Kamm heran, der dann im
dritten Bild dieser Sequenz die Struktur des Gebirges wesentlich bestimmt. Die Bilder
für größeres Delay werden dann ebenfalls von diesem Kamm bestimmt.
Der Einfluss der Kopplung hat gemäß seinem
noch ein Muster
zu sehen ist, in dem die auffälligen Gebiete von dem Punkt, an dem beide Blasen
ihre Resonanzruheradien haben, entfernt sind, nähern sie sich für
abnehmende Kopplung diesem Punkt immer mehr an. Die Kämme der sekundären
Bjerkneskräfte bei den Resonanzradien werden immer deutlicher, bis sie durch die
große Entfernung der Blasen stark abgeschwächt werden. Ein Vergleich der
Abbildungen 3.13 bis 3.15 mit den Abbildungen 3.9 bis 3.11
zeigt eine deutliche Ähnlichkeit. Zunächst liegen die hohen Berge der
Amplituden- Bjerkneskraft-Gebirge weit außen in der betrachteten Ebene, dann
wandern diese Gipfel zum zentralen Punkt, an dem beide Blasen ihren
Resonanzruheradius haben, und von außen wächst ein Kamm heran, der dann im
dritten Bild dieser Sequenz die Struktur des Gebirges wesentlich bestimmt. Die Bilder
für größeres Delay werden dann ebenfalls von diesem Kamm bestimmt.
Der Einfluss der Kopplung hat gemäß seinem 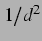 -Abfall stark
abgenommen.
-Abfall stark
abgenommen.
Abbildung: Sekundäre Bjerkneskraft für
delay-gekoppelt schwingende Blasen wie in Abbildung 3.13 sowie ihr Vorzeichen bei
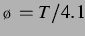 , entspricht
, entspricht
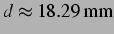 . Der obere abstoßende Bereich ist bei
weitem noch nicht so weit aus dem dargestellten Ausschnitt der
. Der obere abstoßende Bereich ist bei
weitem noch nicht so weit aus dem dargestellten Ausschnitt der 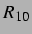 -
-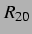 -Ebene gewandert wie in Abbildung 3.4.
-Ebene gewandert wie in Abbildung 3.4.
|
|
Abbildung 3.18: Sekundäre Bjerkneskraft für
delay-gekoppelt schwingende Blasen wie in Abbildung 3.13 sowie ihr Vorzeichen bei  ,
entspricht
,
entspricht
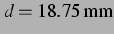 . Die Symmetrie der instantan wechselwirkenden Blasen
ist ,,maximal gebrochen`` (vgl. Abb. 3.5).
. Die Symmetrie der instantan wechselwirkenden Blasen
ist ,,maximal gebrochen`` (vgl. Abb. 3.5).
|
|
Abbildung 3.19: Sekundäre Bjerkneskraft für
delay-gekoppelt schwingende Blasen wie in Abbildung 3.13 sowie ihr Vorzeichen bei 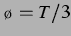 ,
entspricht
,
entspricht 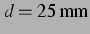 . Zu Abbildung 3.7 ist kein Unterschied in der Verteilung der
Vorzeichen zu erkennen.
. Zu Abbildung 3.7 ist kein Unterschied in der Verteilung der
Vorzeichen zu erkennen.
|
|
Abbildung: Sekundäre Bjerkneskraft für
delay-gekoppelt schwingende Blasen wie in Abbildung 3.13 sowie ihr Vorzeichen bei 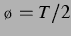 ,
entspricht
,
entspricht
 . Wie in Abschnitt 3.1.2 ist auch hier das Vorzeichen gegenüber
der ersten Abbildung der Serie (3.13)
umgedreht. Für größere
. Wie in Abschnitt 3.1.2 ist auch hier das Vorzeichen gegenüber
der ersten Abbildung der Serie (3.13)
umgedreht. Für größere  wiederholt sich die ganze
Serie wie in Abbildung 3.8
beschrieben.
wiederholt sich die ganze
Serie wie in Abbildung 3.8
beschrieben.
|
|




Nächste Seite: Ergebnisse der
numerischen Simulationen Aufwärts: Die linearisierte Keller-Miksis-Gleichung mit Vorherige
Seite: Theorie Inhalt
Stefan Kamphausen 2003-07-17
![\includegraphics [width=8.5cm]{Linear/kopp_100.ps}](img326.png)
![\includegraphics [width=6.791cm]{Linear/kopp_100_sig.ps}](img327.png)
![\includegraphics [width=8.5cm]{Linear/kopp_100.ps}](img326.png)
![\includegraphics [width=6.791cm]{Linear/kopp_100_sig.ps}](img327.png)
![]() liegen sie
bei bei etwa
liegen sie
bei bei etwa
![]() . Eine Diskussion hierzu findet sich später in diesem
Abschnitt. Da der Unterschied der Abbildungen 3.13 und 3.15
sehr groß ist, wurde noch ein weiterer Wert,
. Eine Diskussion hierzu findet sich später in diesem
Abschnitt. Da der Unterschied der Abbildungen 3.13 und 3.15
sehr groß ist, wurde noch ein weiterer Wert, ![]() in die Serie mit aufgenommen,
um zu betrachten, wie sich die Bjerkneskraftlandschaft bei sehr kleinem Delay
verändert.
in die Serie mit aufgenommen,
um zu betrachten, wie sich die Bjerkneskraftlandschaft bei sehr kleinem Delay
verändert.![\includegraphics [width=8.5cm]{Linear/kopp_50.ps}](img330.png)
![\includegraphics [width=6.791cm]{Linear/kopp_50_sig.ps}](img331.png)
![\includegraphics [width=8.5cm]{Linear/kopp_10.ps}](img333.png)
![\includegraphics [width=6.791cm]{Linear/kopp_10_sig.ps}](img334.png)
![\includegraphics [width=8.5cm]{Linear/kopp_5.ps}](img337.png)
![\includegraphics [width=6.791cm]{Linear/kopp_5_sig.ps}](img338.png)
![]() bis
bis ![]() ähneln denen im Fall
ungekoppelter Blasen. Im Bereich um
ähneln denen im Fall
ungekoppelter Blasen. Im Bereich um ![]() ändert sich das Vorzeichenmuster
sehr schnell und bei
ändert sich das Vorzeichenmuster
sehr schnell und bei ![]() sind die Vorzeichen gerade umgedreht zu denen bei
sind die Vorzeichen gerade umgedreht zu denen bei
![]() . Der Betrag der sekundären Bjerkneskraft ist bei sehr
kleinem Delay größer als bei ungekoppelt schwingenden Blasen, was sich
aber mit zunehmendem Abstand ändert. Der Vergleich mit den Abbildungen 3.9 bis 3.12 aus Abschnitt 3.2.1 erklärt die bereits angesprochene Verteilung
der Extremwerte der sekundären Bjerkneskraft. Dort wurde die Amplitude
. Der Betrag der sekundären Bjerkneskraft ist bei sehr
kleinem Delay größer als bei ungekoppelt schwingenden Blasen, was sich
aber mit zunehmendem Abstand ändert. Der Vergleich mit den Abbildungen 3.9 bis 3.12 aus Abschnitt 3.2.1 erklärt die bereits angesprochene Verteilung
der Extremwerte der sekundären Bjerkneskraft. Dort wurde die Amplitude ![]() der
der ![]() -ten Blase gezeigt, und es wurde festgestellt, dass dieses Muster durch die
abnehmende Kopplung an Komplexität verliert und sich zu einem einfachen Kamm am
Resonanzradius der jeweiligen Blase entwickelt. Dieses Verhalten bestimmt auch
wesentlich die sekundären Bjerkneskraft-Gebirge, bei denen sich ein
ähnliches Verhalten erkennen lässt. Während in der Abbildung 3.13 bei einem Delay von
-ten Blase gezeigt, und es wurde festgestellt, dass dieses Muster durch die
abnehmende Kopplung an Komplexität verliert und sich zu einem einfachen Kamm am
Resonanzradius der jeweiligen Blase entwickelt. Dieses Verhalten bestimmt auch
wesentlich die sekundären Bjerkneskraft-Gebirge, bei denen sich ein
ähnliches Verhalten erkennen lässt. Während in der Abbildung 3.13 bei einem Delay von ![]() noch ein Muster
zu sehen ist, in dem die auffälligen Gebiete von dem Punkt, an dem beide Blasen
ihre Resonanzruheradien haben, entfernt sind, nähern sie sich für
abnehmende Kopplung diesem Punkt immer mehr an. Die Kämme der sekundären
Bjerkneskräfte bei den Resonanzradien werden immer deutlicher, bis sie durch die
große Entfernung der Blasen stark abgeschwächt werden. Ein Vergleich der
Abbildungen 3.13 bis 3.15 mit den Abbildungen 3.9 bis 3.11
zeigt eine deutliche Ähnlichkeit. Zunächst liegen die hohen Berge der
Amplituden- Bjerkneskraft-Gebirge weit außen in der betrachteten Ebene, dann
wandern diese Gipfel zum zentralen Punkt, an dem beide Blasen ihren
Resonanzruheradius haben, und von außen wächst ein Kamm heran, der dann im
dritten Bild dieser Sequenz die Struktur des Gebirges wesentlich bestimmt. Die Bilder
für größeres Delay werden dann ebenfalls von diesem Kamm bestimmt.
Der Einfluss der Kopplung hat gemäß seinem
noch ein Muster
zu sehen ist, in dem die auffälligen Gebiete von dem Punkt, an dem beide Blasen
ihre Resonanzruheradien haben, entfernt sind, nähern sie sich für
abnehmende Kopplung diesem Punkt immer mehr an. Die Kämme der sekundären
Bjerkneskräfte bei den Resonanzradien werden immer deutlicher, bis sie durch die
große Entfernung der Blasen stark abgeschwächt werden. Ein Vergleich der
Abbildungen 3.13 bis 3.15 mit den Abbildungen 3.9 bis 3.11
zeigt eine deutliche Ähnlichkeit. Zunächst liegen die hohen Berge der
Amplituden- Bjerkneskraft-Gebirge weit außen in der betrachteten Ebene, dann
wandern diese Gipfel zum zentralen Punkt, an dem beide Blasen ihren
Resonanzruheradius haben, und von außen wächst ein Kamm heran, der dann im
dritten Bild dieser Sequenz die Struktur des Gebirges wesentlich bestimmt. Die Bilder
für größeres Delay werden dann ebenfalls von diesem Kamm bestimmt.
Der Einfluss der Kopplung hat gemäß seinem ![]() -Abfall stark
abgenommen.
-Abfall stark
abgenommen.![\includegraphics[width=8.5cm]{Linear/kopp_4.1.ps}](img340.png)
![\includegraphics[width=6.791cm]{Linear/kopp_4.1_sig.ps}](img341.png)
![\includegraphics[width=8.5cm]{Linear/kopp_4.ps}](img342.png)
![\includegraphics[width=6.791cm]{Linear/kopp_4_sig.ps}](img343.png)
![\includegraphics[width=8.5cm]{Linear/kopp_3.ps}](img344.png)
![\includegraphics[width=6.791cm]{Linear/kopp_3_sig.ps}](img345.png)
![\includegraphics[width=8.5cm]{Linear/kopp_2.ps}](img346.png)
![\includegraphics[width=6.791cm]{Linear/kopp_2_sig.ps}](img347.png)