



Nächste Seite: Ergebnisse
Aufwärts: Die linearisierte
Keller-Miksis-Gleichung mit Vorherige Seite: Die linearisierte Keller-Miksis-Gleichung mit Inhalt
Theorie
Etwas allgemeiner als in Gleichung (3.2)
lautet die linearisierte Keller-Miksis-Gleichung:
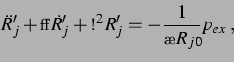
|
(35) |
wobei 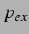 äußere Wechseldruck ist. Es wird auch hier wieder die komplexe
Schreibweise verwendet. Somit gilt für den anregenden Druck der zweiten Blase
(s. Abschnitt 2.1 für den neu
hinzugekommenen Kopplungsterm):
äußere Wechseldruck ist. Es wird auch hier wieder die komplexe
Schreibweise verwendet. Somit gilt für den anregenden Druck der zweiten Blase
(s. Abschnitt 2.1 für den neu
hinzugekommenen Kopplungsterm):
Die linearisierte Keller-Miksis-Gleichung mit Kopplung für die zweite Blase im
Abstand 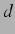 von der ersten lautet also:
von der ersten lautet also:
![\begin{displaymath} \ddot{R}_2' + \alpha_2\dot{R}_2'+\omega_{20}^2R_2' = -\fra... ...R}_{1\tau}^2 + R_{\tau1}^2 \ddot{R}_{1\tau} \right) \right]. \end{displaymath}](img275.png)
|
(36) |
Schwingt nun die erste Blase sinusförmig mit kleiner, reeller Auslenkung 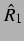 und mit einer Phase
und mit einer Phase 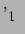 zum anregenden Schallfeld,
zum anregenden Schallfeld,
so gilt mit einem weiteren Phasenfaktor
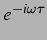 durch die endliche Laufzeit des Schalls am Ort der zweiten
Blase
durch die endliche Laufzeit des Schalls am Ort der zweiten
Blase
Bis auf Terme höherer Ordnung in 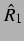 hat nun Gleichung (3.19) die Form
hat nun Gleichung (3.19) die Form
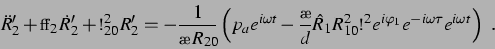
|
(38) |
Die Schwingung von 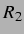 ist ja ebenfalls sinusförmig um ihren Ruheradius
angenommen:
ist ja ebenfalls sinusförmig um ihren Ruheradius
angenommen:
Einsetzen in (3.21) und Umstellen
liefert:
Mit
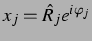 erhält man nun für beide Blasen das
Gleichungssystem
erhält man nun für beide Blasen das
Gleichungssystem
wobei 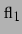 ,
,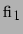 und
und 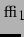 analog zu
analog zu 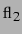 ,
,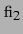 und
und 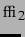 mit vertauschten Indizes
definiert sind. Die Lösung ist:
mit vertauschten Indizes
definiert sind. Die Lösung ist:
Also ist
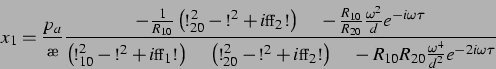
|
(42) |
und 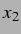 entsprechend.
entsprechend.
Aus 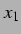 und
und 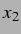 wurden numerisch die Phasen
wurden numerisch die Phasen 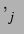 vermöge
vermöge
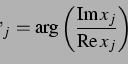
|
(43) |
und die Amplituden 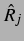 nach
nach
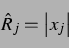 |
(44) |
bestimmt. Anhand Gleichung (3.25) erkennt man,
dass die Amplituden 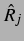 linear mit dem Anregungsdruck
linear mit dem Anregungsdruck 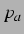 . Die nun folgenden
Gebirgsabbildungen sehen also (wie auch schon vorher beim ungekoppelten Fall)
für beliebige Anregungsdruckamplituden
. Die nun folgenden
Gebirgsabbildungen sehen also (wie auch schon vorher beim ungekoppelten Fall)
für beliebige Anregungsdruckamplituden 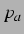 identisch aus, lediglich die
Höhen müssen linear skaliert werden.
identisch aus, lediglich die
Höhen müssen linear skaliert werden.
Um nun einen Eindruck zu bekommen, wie die 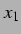 -Landschaft aussieht, zeigt
Abbildung 3.9 die Amplituden der
-Landschaft aussieht, zeigt
Abbildung 3.9 die Amplituden der
 der ersten Blase (links) und
der ersten Blase (links) und
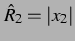 der zweiten Blase (rechts) für
der zweiten Blase (rechts) für  und
und
 . In weiten Gebieten dieser Ebene ist die Amplitude der
Schwingung um den Ruheradius
. In weiten Gebieten dieser Ebene ist die Amplitude der
Schwingung um den Ruheradius 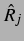 sehr klein. Auf dem Resonanzradius der jeweiligen
Blase jedoch kommt es zu einem extremen Aufschwingen der Blase. Das führt zu
Amplituden, die an einigen Stellen sogar größer als der Ruheradius selbst
sind. An solchen Punkten gilt also die Annahme einer kleinen Schwingung um
sehr klein. Auf dem Resonanzradius der jeweiligen
Blase jedoch kommt es zu einem extremen Aufschwingen der Blase. Das führt zu
Amplituden, die an einigen Stellen sogar größer als der Ruheradius selbst
sind. An solchen Punkten gilt also die Annahme einer kleinen Schwingung um 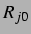 nicht mehr, und die Lösungen werden sogar unphysikalisch (negativer Radius).
Durch die starke Kopplung kommt es auch zu einer stärkeren Schwingung bei der
ersten Blase, wenn die zweite in der Nähe ihres Resonanzradius ist, und
umgekehrt im rechten Bild.
nicht mehr, und die Lösungen werden sogar unphysikalisch (negativer Radius).
Durch die starke Kopplung kommt es auch zu einer stärkeren Schwingung bei der
ersten Blase, wenn die zweite in der Nähe ihres Resonanzradius ist, und
umgekehrt im rechten Bild.
Abbildung: Die Amplituden
 der ersten Blase (links) und
der ersten Blase (links) und
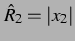 der zweiten Blase (rechts) in der
der zweiten Blase (rechts) in der 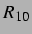 -
-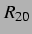 -Ebene bei einem Delay von
-Ebene bei einem Delay von  und
und
 . Man sieht, dass sich die Blasen an ihrer Resonanz
leicht auf das doppelte ihres Ruheradius aufziehen. Dort gilt also die gemachte
Annahme nicht mehr, dass die Blase mit kleiner Amplitude um ihren Ruheradius
schwingt. Es zeigt sich (vgl. Abb. 3.13), dass die Bjerkneskräfte wesentlich
durch diese Größen
. Man sieht, dass sich die Blasen an ihrer Resonanz
leicht auf das doppelte ihres Ruheradius aufziehen. Dort gilt also die gemachte
Annahme nicht mehr, dass die Blase mit kleiner Amplitude um ihren Ruheradius
schwingt. Es zeigt sich (vgl. Abb. 3.13), dass die Bjerkneskräfte wesentlich
durch diese Größen 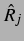 bestimmt werden.
bestimmt werden.
|
|
Abbildung: Die Amplituden
 der ersten Blase (links) und
der ersten Blase (links) und
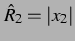 der zweiten Blase (rechts) in der
der zweiten Blase (rechts) in der 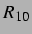 -
-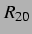 -Ebene bei einem Delay von
-Ebene bei einem Delay von 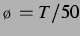 . Das
kreuzförmige Muster aus Abb. 3.9
schließt sich mehr zur Mitte. Die Maxima verschmelzen zu einem Kamm.
. Das
kreuzförmige Muster aus Abb. 3.9
schließt sich mehr zur Mitte. Die Maxima verschmelzen zu einem Kamm.
|
|
Im Falle von kleinem Delay (Abbildungen 3.9 und 3.10)
ergibt sich für 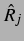 ein kreuzförmiges Muster mit verschiedenen
Maxima. Interessanterweise gibt es gerade dann, wenn beide Blasen auf
Resonanzgröße sind, keine starken Schwingungen, sondern eine Art
,,destruktive Interferenz`` von Anregungs- und Kopplungsdruck (man beachte die
unterschiedlichen Vorzeichen in Gleichung (3.21), rechte Seite). Für größeres
Delay, und damit mit abnehmender Kopplung, zeigen die folgenden Abbildungen (3.11 bis 3.12)
lediglich den vom ungekoppelten Fall her zu erwartenden Kamm beim Resonanzradius der
jeweiligen Blase mit einem Einschnitt, wenn auch die andere Blase ihren
Resonanzruheradius hat. Dies kommt durch die erwähnte Interferenz.
ein kreuzförmiges Muster mit verschiedenen
Maxima. Interessanterweise gibt es gerade dann, wenn beide Blasen auf
Resonanzgröße sind, keine starken Schwingungen, sondern eine Art
,,destruktive Interferenz`` von Anregungs- und Kopplungsdruck (man beachte die
unterschiedlichen Vorzeichen in Gleichung (3.21), rechte Seite). Für größeres
Delay, und damit mit abnehmender Kopplung, zeigen die folgenden Abbildungen (3.11 bis 3.12)
lediglich den vom ungekoppelten Fall her zu erwartenden Kamm beim Resonanzradius der
jeweiligen Blase mit einem Einschnitt, wenn auch die andere Blase ihren
Resonanzruheradius hat. Dies kommt durch die erwähnte Interferenz.
Abbildung: Die Amplituden
 der ersten Blase (links) und
der ersten Blase (links) und
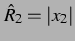 der zweiten Blase (rechts) in der
der zweiten Blase (rechts) in der 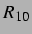 -
-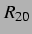 -Ebene bei einem Delay von
-Ebene bei einem Delay von  und einem
Anregungsdruck
und einem
Anregungsdruck
 . Die Kopplung der Blasen hat schon so weit abgenommen,
dass im Wesentlichen ein Kammmuster zu sehen ist, bei dem die Blase an ihrer
Resonanz auf etwa
. Die Kopplung der Blasen hat schon so weit abgenommen,
dass im Wesentlichen ein Kammmuster zu sehen ist, bei dem die Blase an ihrer
Resonanz auf etwa 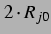 aufschwingt. Für geringere Drücke
ergibt sich aber keine andere Geometrie, da die Amplitude der Schwingung linear
mit
aufschwingt. Für geringere Drücke
ergibt sich aber keine andere Geometrie, da die Amplitude der Schwingung linear
mit 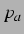 skaliert.
skaliert.
|
|
Wie die letzte Abbildung, Abb. 3.12 zeigt,
wird auch der Einschnitt beim Resonanzradius der benachbarten Blase mit zunehmenden
Abstand immer weiter geglättet. Für großes Delay erhält man ein
beinahe reines Resonanzverhalten, ohne nennenswerten Einfluss der Kopplung.
Abbildung: Die Amplituden
 der ersten Blase (links) und
der ersten Blase (links) und
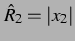 der zweiten Blase (rechts) in der
der zweiten Blase (rechts) in der 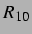 -
-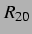 -Ebene bei einem Delay von
-Ebene bei einem Delay von 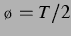 . Die
Amplitude der Schwingung um den Ruheradius zeigt ein beinahe reines
Resonanzverhalten, ohne nennenswerten Einfluss der Kopplung.
. Die
Amplitude der Schwingung um den Ruheradius zeigt ein beinahe reines
Resonanzverhalten, ohne nennenswerten Einfluss der Kopplung.
|
|




Nächste Seite: Ergebnisse
Aufwärts: Die linearisierte
Keller-Miksis-Gleichung mit Vorherige Seite: Die linearisierte Keller-Miksis-Gleichung mit Inhalt
Stefan Kamphausen 2003-07-17
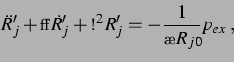
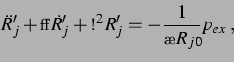
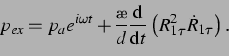

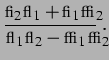
![]() und
und ![]() wurden numerisch die Phasen
wurden numerisch die Phasen ![]() vermöge
vermöge![]() -Landschaft aussieht, zeigt
Abbildung 3.9 die Amplituden der
-Landschaft aussieht, zeigt
Abbildung 3.9 die Amplituden der
![]() der ersten Blase (links) und
der ersten Blase (links) und
![]() der zweiten Blase (rechts) für
der zweiten Blase (rechts) für ![]() und
und
![]() . In weiten Gebieten dieser Ebene ist die Amplitude der
Schwingung um den Ruheradius
. In weiten Gebieten dieser Ebene ist die Amplitude der
Schwingung um den Ruheradius ![]() sehr klein. Auf dem Resonanzradius der jeweiligen
Blase jedoch kommt es zu einem extremen Aufschwingen der Blase. Das führt zu
Amplituden, die an einigen Stellen sogar größer als der Ruheradius selbst
sind. An solchen Punkten gilt also die Annahme einer kleinen Schwingung um
sehr klein. Auf dem Resonanzradius der jeweiligen
Blase jedoch kommt es zu einem extremen Aufschwingen der Blase. Das führt zu
Amplituden, die an einigen Stellen sogar größer als der Ruheradius selbst
sind. An solchen Punkten gilt also die Annahme einer kleinen Schwingung um ![]() nicht mehr, und die Lösungen werden sogar unphysikalisch (negativer Radius).
Durch die starke Kopplung kommt es auch zu einer stärkeren Schwingung bei der
ersten Blase, wenn die zweite in der Nähe ihres Resonanzradius ist, und
umgekehrt im rechten Bild.
nicht mehr, und die Lösungen werden sogar unphysikalisch (negativer Radius).
Durch die starke Kopplung kommt es auch zu einer stärkeren Schwingung bei der
ersten Blase, wenn die zweite in der Nähe ihres Resonanzradius ist, und
umgekehrt im rechten Bild.![\includegraphics [width=7.0cm]{Linear/reso_kopp_100_1.ps}](img317.png)
![\includegraphics [width=7.0cm]{Linear/reso_kopp_100_2.ps}](img318.png)
![\includegraphics [width=7.0cm]{Linear/reso_kopp_50_1.ps}](img319.png)
![\includegraphics [width=7.0cm]{Linear/reso_kopp_50_2.ps}](img320.png)
![]() ein kreuzförmiges Muster mit verschiedenen
Maxima. Interessanterweise gibt es gerade dann, wenn beide Blasen auf
Resonanzgröße sind, keine starken Schwingungen, sondern eine Art
,,destruktive Interferenz`` von Anregungs- und Kopplungsdruck (man beachte die
unterschiedlichen Vorzeichen in Gleichung (3.21), rechte Seite). Für größeres
Delay, und damit mit abnehmender Kopplung, zeigen die folgenden Abbildungen (3.11 bis 3.12)
lediglich den vom ungekoppelten Fall her zu erwartenden Kamm beim Resonanzradius der
jeweiligen Blase mit einem Einschnitt, wenn auch die andere Blase ihren
Resonanzruheradius hat. Dies kommt durch die erwähnte Interferenz.
ein kreuzförmiges Muster mit verschiedenen
Maxima. Interessanterweise gibt es gerade dann, wenn beide Blasen auf
Resonanzgröße sind, keine starken Schwingungen, sondern eine Art
,,destruktive Interferenz`` von Anregungs- und Kopplungsdruck (man beachte die
unterschiedlichen Vorzeichen in Gleichung (3.21), rechte Seite). Für größeres
Delay, und damit mit abnehmender Kopplung, zeigen die folgenden Abbildungen (3.11 bis 3.12)
lediglich den vom ungekoppelten Fall her zu erwartenden Kamm beim Resonanzradius der
jeweiligen Blase mit einem Einschnitt, wenn auch die andere Blase ihren
Resonanzruheradius hat. Dies kommt durch die erwähnte Interferenz.![\includegraphics [width=7.0cm]{Linear/reso_kopp_10_1.ps}](img321.png)
![\includegraphics [width=7.0cm]{Linear/reso_kopp_10_2.ps}](img322.png)
![\includegraphics [width=7.0cm]{Linear/reso_kopp_2_1.ps}](img323.png)
![\includegraphics [width=7.0cm]{Linear/reso_kopp_2_2.ps}](img324.png)