



Nächste Seite: Zusammenfassung
und Ausblick Aufwärts: diplom Vorherige Seite: Sekundäre Bjerkneskraft bei für Inhalt
Ausgewählte Trajektorien von Kavitationsblasen
Nachdem in den vorherigen Kapiteln der Schwerpunkt auf der sekundären
Bjerkneskraft lag, werden nun einige Einzelheiten der Kavitationsblasendynamik
betrachtet. Diese sollen den Hintergrund der sekundären Bjerkneskraft, die
eigentliche Blasenschwingung, näher beleuchten und so Anhaltspunkte zur
Erklärung des einen oder anderen Ergebnisses liefern. Es wurden noch mehr
Effekte beobachtet, als letztlich hier vorgestellt werden. So fanden sich
,,super-resonante`` Blasenpaare, bei denen sich die Blasen gegenseitig aufschaukeln
und die die großen Gebirge in Abbildung 4.9 erklären können. Diese werden hier jedoch
nicht mehr besprochen, sondern werden in zukünftigen Arbeiten betrachtet werden.
Für die drei verwendeten Modelle, deren Ergebnisse im Laufe dieser Arbeit
vorgestellt wurden, werden einige Trajektorien von 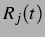 gezeigt.
gezeigt.
Das lineare Modell setzt in beiden Fällen eine kleine, harmonische Schwingung
der 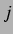 -ten Blase um ihren Ruheradius vorraus:
-ten Blase um ihren Ruheradius vorraus:
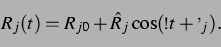
|
(46) |
Im ungekoppelten Fall, der in Abschnitt 3.1
genauer beschrieben wurde, ergeben sich 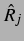 und
und 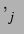 zu
zu
während man diese Größen im delay-gekoppelt schwingenden Fall
vermöge
mit dem in Abschnitt 3.2 beschriebenen 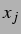 berechnet.
berechnet.
Die Schwingung des vollen nichtlinearen Modells ergibt sich aus der numerischen
Simulation.
Die folgenden Abbildungen zeigen jeweils bei drei verschiedenen Drücken (von
links nach rechts:
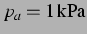 ,
,
 und
und
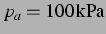 , wie sie auch in Kapitel 4 verwendet wurden) die
, wie sie auch in Kapitel 4 verwendet wurden) die 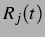 -Trajektorien einer Blase, wie sie
sich nach den drei Modellen berechnen. Ganz oben sieht man das lineare, ungekoppelte
Modell, darunter das lineare, gekoppelte und unten schließlich das nichtlineare
Modell.
-Trajektorien einer Blase, wie sie
sich nach den drei Modellen berechnen. Ganz oben sieht man das lineare, ungekoppelte
Modell, darunter das lineare, gekoppelte und unten schließlich das nichtlineare
Modell.
Eine Blase eines Blasenpaares mit Radien weit entfernt von ihrer Resonanz und
nicht sehr unterschiedlich (
 und
und
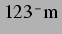 ) wird in den Abbildungen 5.1 (für ein Delay
) wird in den Abbildungen 5.1 (für ein Delay  ) und 5.2 (
) und 5.2 ( ) gezeigt. Dort ergibt sich
unabhängig vom Delay eine gute Übereinstimmung beider linearer Modelle mit
dem nichtlinearen Modell, solange der Schalldruck der Anregung nicht zu groß
wird.
) gezeigt. Dort ergibt sich
unabhängig vom Delay eine gute Übereinstimmung beider linearer Modelle mit
dem nichtlinearen Modell, solange der Schalldruck der Anregung nicht zu groß
wird.
Abbildung 5.1: 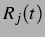 -Trajektorien bei
-Trajektorien bei  ,
,
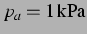 (links),
(links),
 (Mitte) und
(Mitte) und
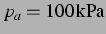 (rechts) für einen Ruheradius weit entfernt von der
linearen Resonanz bei
(rechts) für einen Ruheradius weit entfernt von der
linearen Resonanz bei
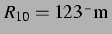 . Die in
. Die in
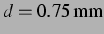 schwingende Nachbarblase hat einen Ruheradius
schwingende Nachbarblase hat einen Ruheradius
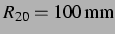 . Gute Übereinstimmung beider linearer Modelle mit
dem nichtlinearen Modell bei geringen Drücken.
. Gute Übereinstimmung beider linearer Modelle mit
dem nichtlinearen Modell bei geringen Drücken.
|
|
Abbildung: Trajektorien bei  ,
,
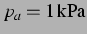 (links),
(links),
 (Mitte) und
(Mitte) und
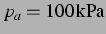 (rechts) für einen Ruheradius weit entfernt von der
linearen Resonanz (
(rechts) für einen Ruheradius weit entfernt von der
linearen Resonanz (
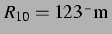 ). Nachbarblase:
). Nachbarblase:
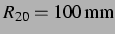 , in
, in
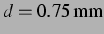 Entfernung. Auch bei größerem Delay eine
gute Übereinstimmung beider linearer Modelle mit dem nichtlinearen Modell
bei geringen Drücken.
Entfernung. Auch bei größerem Delay eine
gute Übereinstimmung beider linearer Modelle mit dem nichtlinearen Modell
bei geringen Drücken.
|
|
Abbildung 5.3 zeigt nun bei einem
kleinen Delay von  die nach den drei im Laufe der Arbeit betrachteten
Modellen berechneten
die nach den drei im Laufe der Arbeit betrachteten
Modellen berechneten 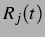 -Kurve einer Blase, deren Ruheradius mit
-Kurve einer Blase, deren Ruheradius mit
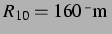 leicht neben der (linearen) Resonanz liegt. Die
angekoppelte Blase, die mit
leicht neben der (linearen) Resonanz liegt. Die
angekoppelte Blase, die mit
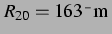 , also recht genau am linearen Resonanzradius, angenommen
wird, wird weiter unten gezeigt, in den Abbildungen 5.5 und Abb. 5.6. Der Abstand ergibt sich aus dem jeweiligen
Delay.
, also recht genau am linearen Resonanzradius, angenommen
wird, wird weiter unten gezeigt, in den Abbildungen 5.5 und Abb. 5.6. Der Abstand ergibt sich aus dem jeweiligen
Delay.
Abbildung 5.3: Trajektorien bei  ,
,
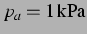 (links),
(links),
 (Mitte) und
(Mitte) und
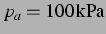 (rechts). Der Ruheradius dieser Blase liegt mit
(rechts). Der Ruheradius dieser Blase liegt mit
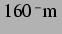 leicht neben der (linearen) Resonanz. In einer Entfernung
von
leicht neben der (linearen) Resonanz. In einer Entfernung
von
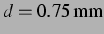 liegt die Nachbarblase mit einem Ruheradius
liegt die Nachbarblase mit einem Ruheradius
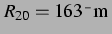 . Das ungekoppelte, lineare Modell liefert schon bei
niedrigem Druck keine sehr gute Übereinstimmung, während das
delay-gekoppelte, lineare Modell noch bei
. Das ungekoppelte, lineare Modell liefert schon bei
niedrigem Druck keine sehr gute Übereinstimmung, während das
delay-gekoppelte, lineare Modell noch bei
 sehr gut mit dem nichtlinearen Modell einhergeht. Bei
noch höherem Druck ergeben sich nach den linearen Modellen unphysikalische
negative Blasenradien. Bei den Trajektorien des nichtlinearen Modells ist zu
erkennen, dass der Zustand nicht vollständig eingeschwungen ist.
sehr gut mit dem nichtlinearen Modell einhergeht. Bei
noch höherem Druck ergeben sich nach den linearen Modellen unphysikalische
negative Blasenradien. Bei den Trajektorien des nichtlinearen Modells ist zu
erkennen, dass der Zustand nicht vollständig eingeschwungen ist.
|
|
Es zeigt sich, dass das lineare Modell bereits bei einem sehr geringen Druck nicht
sehr exakte Werte liefert, während die Voraussagen des linearen Modells, das die
Delaykopplung mit einbezieht, sehr gut an den Werten des nichtlinearen Modells
liegen. Es fällt sofort die fast entgegengesetzte Phase zwischen gekoppeltem und
ungekoppeltem Modell auf. Bei den betrachteten Ruheradien dich bei der linearen
Resonanz hat die Kopplung offenbar eine sehr große Wirkung. Die ungekoppelte
Näherung liefert auch bei kleinen Drücken schon große
Schwingungsamplituden. Bei höheren Druckwerten entstehen bei beiden linearen
Näherungen negative Radien, was physikalisch nicht sinnvoll ist. Es fällt
auf, dass die Trajektorien des nichtlinearen Modells nicht eingeschwungen sind.
Tatsächlich ergibt sich für dieses Blasenpaar eine quasiperiodische
Schwingung bei einer sehr langen Transiente bis zur nichtlinearen Sättigung. Die
Schwingungsform, die sich für die Blase bei hohem Druck ergibt, lässt sich
natürlich mit einer harmonischen Schwingung nicht mehr darstellen.
Abbildung 5.4 zeigt die Blasenschwingung
bei gleichem Druck, aber größerem Delay  . Auf den ungekoppelten Fall
hat das Delay keinen Einfluss, doch die Amplitude stimmt mit dem nichtlinearen Fall
jetzt besser überein. Bei
. Auf den ungekoppelten Fall
hat das Delay keinen Einfluss, doch die Amplitude stimmt mit dem nichtlinearen Fall
jetzt besser überein. Bei
 schwingt die Blase im vollen Modell bereits nicht mehr
harmonisch, so dass auch zum linearen, gekoppelten Modell ein Unterschied zu sehen
ist. Dessen Amplitude trifft aber noch recht gut zu. Bei hohem Druck weichen beide
lineare Modelle noch mehr vom nichtlinearen Modell ab, als das bei
schwingt die Blase im vollen Modell bereits nicht mehr
harmonisch, so dass auch zum linearen, gekoppelten Modell ein Unterschied zu sehen
ist. Dessen Amplitude trifft aber noch recht gut zu. Bei hohem Druck weichen beide
lineare Modelle noch mehr vom nichtlinearen Modell ab, als das bei  der Fall
war.
der Fall
war.
Abbildung: Trajektorien bei  ,
,
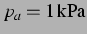 (links),
(links),
 (Mitte) und
(Mitte) und
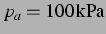 (rechts) für eine Blase mit einem Ruheradius
(rechts) für eine Blase mit einem Ruheradius
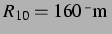 . Die Nachbarblase mit
. Die Nachbarblase mit
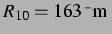 schwingt in
schwingt in
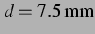 Entfernung. Bei
Entfernung. Bei
 schwingt die Blase bereits nicht mehr harmonisch. Die
Abweichung bei
schwingt die Blase bereits nicht mehr harmonisch. Die
Abweichung bei
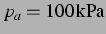 ist noch größer als in Abb. 5.3.
ist noch größer als in Abb. 5.3.
|
|
Die zweite Blase dieses Paares (
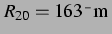 ) wird in den Abbildungen 5.5 und 5.6, wieder für
) wird in den Abbildungen 5.5 und 5.6, wieder für  und
und  gezeigt.
Dort liefern beide lineare Modelle bei
gezeigt.
Dort liefern beide lineare Modelle bei  eine ähnlich gute Trajektorie,
im Sinne einer guten Übereinstimmung mit dem nichtlinearen Modell, für
eine ähnlich gute Trajektorie,
im Sinne einer guten Übereinstimmung mit dem nichtlinearen Modell, für
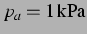 , während sie bei
, während sie bei
 bereits negative Radien angeben. Bei
bereits negative Radien angeben. Bei  liefert das
delay-gekoppelte Modell dagegen für
liefert das
delay-gekoppelte Modell dagegen für
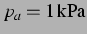 und
und
 noch gute Werte.
noch gute Werte.
Abbildung 5.5: Trajektorien bei  (
(
 ),
),
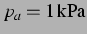 (links),
(links),
 (Mitte) und
(Mitte) und
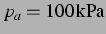 (rechts) für die zweite Blase des Paares mit einem
Ruheradius von
(rechts) für die zweite Blase des Paares mit einem
Ruheradius von
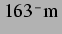 (sehr genau auf dem linearen Resonanzradius). Das
ungekoppelte Modell liegt sehr weit neben den Werten des nichtlinearen Modells,
dessen Zustand nicht richtig eingeschwungen ist; das delay-gekoppelte Modell
beschreibt die Blasenschwingung gut für geringe Drücke.
(sehr genau auf dem linearen Resonanzradius). Das
ungekoppelte Modell liegt sehr weit neben den Werten des nichtlinearen Modells,
dessen Zustand nicht richtig eingeschwungen ist; das delay-gekoppelte Modell
beschreibt die Blasenschwingung gut für geringe Drücke.
|
|
Abbildung 5.6: Trajektorien bei  (
( ),
),
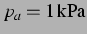 (links),
(links),
 (Mitte) und
(Mitte) und
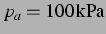 (rechts) für die zweite Blase des Paares mit einem
Ruheradius von
(rechts) für die zweite Blase des Paares mit einem
Ruheradius von
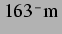 . Gute Übereinstimmung aller drei Modelle bei sehr
geringem Druck, aber die beiden linearen versagen bereits bei
. Gute Übereinstimmung aller drei Modelle bei sehr
geringem Druck, aber die beiden linearen versagen bereits bei
 .
.
|
|
Es zeigt sich also, dass die Blasenschwingung in der Nähe der linearen
Resonanz stark von Kopplung und Delay abhängt. Dort sind auch die linearen
Näherungen nicht mehr verlässlich, was nicht verwunderlich ist, schwingen
die Blasen doch teilweise mit beträchtlichen Amplituden um ihren Ruheradius.
Dass die Abweichungen des ungekoppelten Modells gegenüber den beiden
delay-gekoppelten Modellen bei  für die Blasen mit einem Ruheradius in der
Nähe ihrer Resonanz größer sind, versteht man, wenn man die
Abbildungen der Schwingungsamplituden in Kapitel 3.2.1 betrachtet. Bei kleinem Delay sind die
Resonanzradien des gekoppelten Modells weit weg von den Resonanzradien des
ungekoppelten Modells, während sie mit zunehmenden Delay immer näher
rücken (vgl. Abb. 3.9 und
Abb. 3.11), da der Einfluss der Kopplung
mit zunehmenden Abstand abnimmt. Somit macht das ungekoppelte Modell in diesem
Bereich bei kleinerem Delay einen größeren Fehler. Bei Ruheradien, die
sehr weit von diesen bezüglich des Delays empfindlichen Bereichen liegen, wie es
in Abbildung 5.1 und Abbildung 5.2 gezeigt wird, sind die Ergebnisse beider
linearen Modelle ähnlich und in guter Übereinstimmung mit der nichtlinearen
Theorie.
für die Blasen mit einem Ruheradius in der
Nähe ihrer Resonanz größer sind, versteht man, wenn man die
Abbildungen der Schwingungsamplituden in Kapitel 3.2.1 betrachtet. Bei kleinem Delay sind die
Resonanzradien des gekoppelten Modells weit weg von den Resonanzradien des
ungekoppelten Modells, während sie mit zunehmenden Delay immer näher
rücken (vgl. Abb. 3.9 und
Abb. 3.11), da der Einfluss der Kopplung
mit zunehmenden Abstand abnimmt. Somit macht das ungekoppelte Modell in diesem
Bereich bei kleinerem Delay einen größeren Fehler. Bei Ruheradien, die
sehr weit von diesen bezüglich des Delays empfindlichen Bereichen liegen, wie es
in Abbildung 5.1 und Abbildung 5.2 gezeigt wird, sind die Ergebnisse beider
linearen Modelle ähnlich und in guter Übereinstimmung mit der nichtlinearen
Theorie.
Es lässt sich also festhalten, dass das ungekoppelte, lineare Modell
über weite Strecken annehmbare Ergebnisse produziert, aber andernorts das System
der zwei Blasen völlig unzureichend modelliert. Das delay-gekoppelte und
linearisierte Modell beschreibt das nichtlineare System, solange dies
tatsächlich harmonisch schwingt, exakter.




Nächste Seite: Zusammenfassung
und Ausblick Aufwärts: diplom Vorherige Seite: Sekundäre Bjerkneskraft bei für Inhalt
Stefan Kamphausen 2003-07-17
![]() ,
,
![]() und
und
![]() , wie sie auch in Kapitel 4 verwendet wurden) die
, wie sie auch in Kapitel 4 verwendet wurden) die ![]() -Trajektorien einer Blase, wie sie
sich nach den drei Modellen berechnen. Ganz oben sieht man das lineare, ungekoppelte
Modell, darunter das lineare, gekoppelte und unten schließlich das nichtlineare
Modell.
-Trajektorien einer Blase, wie sie
sich nach den drei Modellen berechnen. Ganz oben sieht man das lineare, ungekoppelte
Modell, darunter das lineare, gekoppelte und unten schließlich das nichtlineare
Modell.![]() und
und
![]() ) wird in den Abbildungen 5.1 (für ein Delay
) wird in den Abbildungen 5.1 (für ein Delay ![]() ) und 5.2 (
) und 5.2 (![]() ) gezeigt. Dort ergibt sich
unabhängig vom Delay eine gute Übereinstimmung beider linearer Modelle mit
dem nichtlinearen Modell, solange der Schalldruck der Anregung nicht zu groß
wird.
) gezeigt. Dort ergibt sich
unabhängig vom Delay eine gute Übereinstimmung beider linearer Modelle mit
dem nichtlinearen Modell, solange der Schalldruck der Anregung nicht zu groß
wird.![\includegraphics [width=5.0cm]{Linear/tra_nokopp_100_0.01_3.ps}](img472.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_100_0.1_3.ps}](img473.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_100_1.0_3.ps}](img474.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_100_0.01_3.ps}](img475.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_100_0.1_3.ps}](img476.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_100_1.0_3.ps}](img477.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_100_0.01_3.ps}](img478.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_100_0.1_3.ps}](img479.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_100_1.0_3.ps}](img480.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_10_0.01_3.ps}](img483.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_10_0.1_3.ps}](img484.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_10_1.0_3.ps}](img485.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_10_0.01_3.ps}](img486.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_10_0.1_3.ps}](img487.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_10_1.0_3.ps}](img488.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_10_0.01_3.ps}](img489.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_10_0.1_3.ps}](img490.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_10_1.0_3.ps}](img491.png)
![]() die nach den drei im Laufe der Arbeit betrachteten
Modellen berechneten
die nach den drei im Laufe der Arbeit betrachteten
Modellen berechneten ![]() -Kurve einer Blase, deren Ruheradius mit
-Kurve einer Blase, deren Ruheradius mit
![]() leicht neben der (linearen) Resonanz liegt. Die
angekoppelte Blase, die mit
leicht neben der (linearen) Resonanz liegt. Die
angekoppelte Blase, die mit
![]() , also recht genau am linearen Resonanzradius, angenommen
wird, wird weiter unten gezeigt, in den Abbildungen 5.5 und Abb. 5.6. Der Abstand ergibt sich aus dem jeweiligen
Delay.
, also recht genau am linearen Resonanzradius, angenommen
wird, wird weiter unten gezeigt, in den Abbildungen 5.5 und Abb. 5.6. Der Abstand ergibt sich aus dem jeweiligen
Delay.![\includegraphics [width=5.0cm]{Linear/tra_nokopp_100_0.01_1.ps}](img494.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_100_0.1_1.ps}](img495.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_100_1.0_1.ps}](img496.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_100_0.01_1.ps}](img497.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_100_0.1_1.ps}](img498.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_100_1.0_1.ps}](img499.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_100_0.01_1.ps}](img500.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_100_0.1_1.ps}](img501.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_100_1.0_1.ps}](img502.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_10_0.01_1.ps}](img503.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_10_0.1_1.ps}](img504.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_10_1.0_1.ps}](img505.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_10_0.01_1.ps}](img506.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_10_0.1_1.ps}](img507.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_10_1.0_1.ps}](img508.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_10_0.01_1.ps}](img509.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_10_0.1_1.ps}](img510.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_10_1.0_1.ps}](img511.png)
![]() ) wird in den Abbildungen 5.5 und 5.6, wieder für
) wird in den Abbildungen 5.5 und 5.6, wieder für ![]() und
und ![]() gezeigt.
Dort liefern beide lineare Modelle bei
gezeigt.
Dort liefern beide lineare Modelle bei ![]() eine ähnlich gute Trajektorie,
im Sinne einer guten Übereinstimmung mit dem nichtlinearen Modell, für
eine ähnlich gute Trajektorie,
im Sinne einer guten Übereinstimmung mit dem nichtlinearen Modell, für
![]() , während sie bei
, während sie bei
![]() bereits negative Radien angeben. Bei
bereits negative Radien angeben. Bei ![]() liefert das
delay-gekoppelte Modell dagegen für
liefert das
delay-gekoppelte Modell dagegen für
![]() und
und
![]() noch gute Werte.
noch gute Werte.![\includegraphics [width=5.0cm]{Linear/tra_nokopp_100_0.01_2.ps}](img513.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_100_0.1_2.ps}](img514.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_100_1.0_2.ps}](img515.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_100_0.01_2.ps}](img516.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_100_0.1_2.ps}](img517.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_100_1.0_2.ps}](img518.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_100_0.01_2.ps}](img519.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_100_0.1_2.ps}](img520.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_100_1.0_2.ps}](img521.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_10_0.01_2.ps}](img523.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_10_0.1_2.ps}](img524.png)
![\includegraphics [width=5.0cm]{Linear/tra_nokopp_10_1.0_2.ps}](img525.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_10_0.01_2.ps}](img526.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_10_0.1_2.ps}](img527.png)
![\includegraphics [width=5.0cm]{Linear/tra_kopp_10_1.0_2.ps}](img528.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_10_0.01_2.ps}](img529.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_10_0.1_2.ps}](img530.png)
![\includegraphics [width=5.0cm]{DKLAG_Tra/dklag_tra_10_1.0_2.ps}](img531.png)
![]() für die Blasen mit einem Ruheradius in der
Nähe ihrer Resonanz größer sind, versteht man, wenn man die
Abbildungen der Schwingungsamplituden in Kapitel 3.2.1 betrachtet. Bei kleinem Delay sind die
Resonanzradien des gekoppelten Modells weit weg von den Resonanzradien des
ungekoppelten Modells, während sie mit zunehmenden Delay immer näher
rücken (vgl. Abb. 3.9 und
Abb. 3.11), da der Einfluss der Kopplung
mit zunehmenden Abstand abnimmt. Somit macht das ungekoppelte Modell in diesem
Bereich bei kleinerem Delay einen größeren Fehler. Bei Ruheradien, die
sehr weit von diesen bezüglich des Delays empfindlichen Bereichen liegen, wie es
in Abbildung 5.1 und Abbildung 5.2 gezeigt wird, sind die Ergebnisse beider
linearen Modelle ähnlich und in guter Übereinstimmung mit der nichtlinearen
Theorie.
für die Blasen mit einem Ruheradius in der
Nähe ihrer Resonanz größer sind, versteht man, wenn man die
Abbildungen der Schwingungsamplituden in Kapitel 3.2.1 betrachtet. Bei kleinem Delay sind die
Resonanzradien des gekoppelten Modells weit weg von den Resonanzradien des
ungekoppelten Modells, während sie mit zunehmenden Delay immer näher
rücken (vgl. Abb. 3.9 und
Abb. 3.11), da der Einfluss der Kopplung
mit zunehmenden Abstand abnimmt. Somit macht das ungekoppelte Modell in diesem
Bereich bei kleinerem Delay einen größeren Fehler. Bei Ruheradien, die
sehr weit von diesen bezüglich des Delays empfindlichen Bereichen liegen, wie es
in Abbildung 5.1 und Abbildung 5.2 gezeigt wird, sind die Ergebnisse beider
linearen Modelle ähnlich und in guter Übereinstimmung mit der nichtlinearen
Theorie.