



Nächste Seite: Ausgewählte
Trajektorien von Kavitationsblasen Aufwärts: Ergebnisse der numerischen Simulationen Vorherige
Seite: Sekundäre Bjerkneskraft bei
hohem Inhalt
Sekundäre Bjerkneskraft bei für die Strukturbildung relevanten
Parametern
Nachdem nun die Vergleiche des vollen nichtlinearen Modells mit der linearen
Näherung gezogen wurden, wird die Bjerkneskraft auch für solche Parameter
berechnet, wie sie in der Strukturbildung tatsächlich auftreten. Wie in
Kapitel 2 beschrieben wurde, liegt die
Größenordnung der Ruheradien der an der Strukturbildung beteiligten Blasen
im Bereich weniger Mikrometer. Daher wird hier nun ein Ausschnitt bei
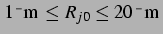 aus der
aus der 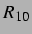 -
-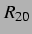 -Ebene gezeigt. Die Auswahl
der berechneten Anregungsdrücke orientiert sich an den in [25] verwendeten:
-Ebene gezeigt. Die Auswahl
der berechneten Anregungsdrücke orientiert sich an den in [25] verwendeten: 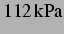 ,
,  ,
, 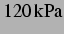 ,
,
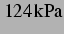 und
und  . Allesamt sind das Drücke, bei denen
Strukturbildung beobachtet werden kann. Außerdem wurden hier nicht mehr die
ganzen
. Allesamt sind das Drücke, bei denen
Strukturbildung beobachtet werden kann. Außerdem wurden hier nicht mehr die
ganzen 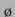 -Serien aufgenommen, sondern nur noch für
-Serien aufgenommen, sondern nur noch für  als sehr kleinem
Delay,
als sehr kleinem
Delay,  für ein weiteres und
für ein weiteres und  , um den ,,unsymmetrischsten`` Punkt,
wie er in Abschnitt 3.1.2 beschrieben
wurde, zu betrachten. Die Auflösung der Abbildungen ist noch etwas geringer als
dies in den vorherigen Abschnitten der Fall war. Daher treten die
Interpolationseffekte deutlicher in Erscheinung.
, um den ,,unsymmetrischsten`` Punkt,
wie er in Abschnitt 3.1.2 beschrieben
wurde, zu betrachten. Die Auflösung der Abbildungen ist noch etwas geringer als
dies in den vorherigen Abschnitten der Fall war. Daher treten die
Interpolationseffekte deutlicher in Erscheinung.
In [25] wurde von METTIN et
al. für instantan gekoppelte Blasen im Abstand von  bei obigen
Anregungsdrücken und ansonsten identischen Parametern (s. Tabelle 2.1) der Bjerkneskoeffizient, der dort als
bei obigen
Anregungsdrücken und ansonsten identischen Parametern (s. Tabelle 2.1) der Bjerkneskoeffizient, der dort als
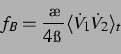
|
(45) |
definiert wurde, berechnet. Der 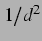 -Abfall der eigentlichen sekundären Bjerkneskraft
wurde nicht beachtet, während hier die tatsächlichen Kräfte
dargestellt werden. Die Vorzeichenmuster in dieser Arbeit sind aber ohne weiteres mit
den Darstellungen aus [25] vergleichbar. Es
zeigte sich dort, dass bei Drücken knapp über
-Abfall der eigentlichen sekundären Bjerkneskraft
wurde nicht beachtet, während hier die tatsächlichen Kräfte
dargestellt werden. Die Vorzeichenmuster in dieser Arbeit sind aber ohne weiteres mit
den Darstellungen aus [25] vergleichbar. Es
zeigte sich dort, dass bei Drücken knapp über 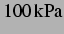 ein zur
Winkelhalbierenden symmetrisches aber ansonsten sehr fein strukturiertes,
fächerförmiges Muster sichtbar wird, in dem sich anziehende und
abstoßende Kräfte bereits bei kleiner Änderung eines Ruheradius
abwechseln. Mit wachsendem Anregungsdruck wachsen abstoßende Bereiche, die
immer schärfer begrenzt sind. Für großen Anregungsdruck (
ein zur
Winkelhalbierenden symmetrisches aber ansonsten sehr fein strukturiertes,
fächerförmiges Muster sichtbar wird, in dem sich anziehende und
abstoßende Kräfte bereits bei kleiner Änderung eines Ruheradius
abwechseln. Mit wachsendem Anregungsdruck wachsen abstoßende Bereiche, die
immer schärfer begrenzt sind. Für großen Anregungsdruck ( )
zeigt das Bild einen sehr großen anziehenden Bereich, wenn beide
)
zeigt das Bild einen sehr großen anziehenden Bereich, wenn beide
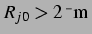 sind. Falls ein Ruheradius größer als
sind. Falls ein Ruheradius größer als 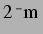 ist und der andere kleiner, ergibt sich eine abstoßende
Kraft, und falls beide kleiner als
ist und der andere kleiner, ergibt sich eine abstoßende
Kraft, und falls beide kleiner als 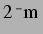 sind, eine anziehende Kraft, deren Betrag
nicht so groß ist wie der der Kraft bei
sind, eine anziehende Kraft, deren Betrag
nicht so groß ist wie der der Kraft bei
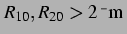 . Es wurde beobachtet, dass die Grenze der
abstoßenden Bereiche, die im beschriebenen Fall von
. Es wurde beobachtet, dass die Grenze der
abstoßenden Bereiche, die im beschriebenen Fall von
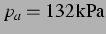 bei
bei
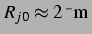 liegt, für zunehmende Drücke von
größeren Ruheradien (etwa
liegt, für zunehmende Drücke von
größeren Ruheradien (etwa 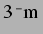 bei
bei
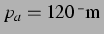 ) zu kleineren Ruheradien geht.
) zu kleineren Ruheradien geht.
Diese Ergebnisse lassen sich mit den im Rahmen dieser Arbeit durchgeführten
Simulationsrechnungen, denen das volle nichtlineare, delay-gekoppelte System zugrunde
liegt, zum Teil wiederfinden. Es zeigen sich aber auch ganz erhebliche Unterschiede
zu den in [25] erzielten Ergebnissen, die im
Folgenden vorgestellt werden.
Abbildung 4.25: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  (
(
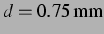 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
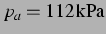 . Bis auf kleine Bereiche, wenn eine der Blasen einen
kleinen Ruheradius hat, ist die Bjerkneskraft anziehend. Diese Geometrie der
Vorzeichenverteilung findet sich bei METTIN et al. in [25] erst bei intensiveren Anregungen. Man
beachte auch die Einheit der sekundären Bjerkneskraft: bei
. Bis auf kleine Bereiche, wenn eine der Blasen einen
kleinen Ruheradius hat, ist die Bjerkneskraft anziehend. Diese Geometrie der
Vorzeichenverteilung findet sich bei METTIN et al. in [25] erst bei intensiveren Anregungen. Man
beachte auch die Einheit der sekundären Bjerkneskraft: bei  jedesmal
jedesmal 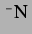 , sonst
, sonst 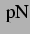 .
.
|
|
Die Abbildungen 4.25 bis 4.27 zeigen die Bjerkneskraft sowie ihr Vorzeichen in
gewohnter Manier bei einem anregenden Schalldruck von 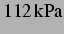 . Entgegen den
Ergebnissen in [25] ist das sich ergebene
Muster in 4.25 bei
. Entgegen den
Ergebnissen in [25] ist das sich ergebene
Muster in 4.25 bei  jedoch nicht
fächerförmig. Es ähnelt eher dem dort für hohe Drücke
gefundenem. Weite Teile des dargestellten Bereichs sind anziehend, bis auf Gebiete,
in denen einer der beiden Ruheradien etwa zwischen
jedoch nicht
fächerförmig. Es ähnelt eher dem dort für hohe Drücke
gefundenem. Weite Teile des dargestellten Bereichs sind anziehend, bis auf Gebiete,
in denen einer der beiden Ruheradien etwa zwischen 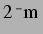 und
und 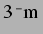 liegt.
Eine geringe Asymmetrie ist zu erkennen.
liegt.
Eine geringe Asymmetrie ist zu erkennen.
Abbildung 4.26: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  (
(
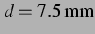 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
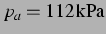 . Eine mehr oder weniger zur Winkelhalbierenden
symmetrische Verteilung der Vorzeichen bei stärkerer Kraft als bei
. Eine mehr oder weniger zur Winkelhalbierenden
symmetrische Verteilung der Vorzeichen bei stärkerer Kraft als bei  .
.
|
|
Die nächsten beiden Bilder 4.26
und 4.27 dieser Serie zeigen dann eine
völlige Auflösung dieser Geometrie. Zunächst kann man bei  noch
eine gebrochene Symmetrie erkennen, ähnlich wie für
noch
eine gebrochene Symmetrie erkennen, ähnlich wie für  zu erwarten. Bei
zu erwarten. Bei
 jedoch ergibt sich in weiten Teilen eine abstoßende Kraft, mit
einigen, keine erkennbare Symmetrie ergebenden, anziehenden ,,Inseln``.
jedoch ergibt sich in weiten Teilen eine abstoßende Kraft, mit
einigen, keine erkennbare Symmetrie ergebenden, anziehenden ,,Inseln``.
Abbildung: Sekundäre Bjerkneskraft aus der nichtlinearen
Simulation und ihr Vorzeichen bei  (
(
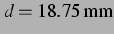 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
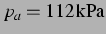 . Ohne erkennbare Symmetrie verteilte anziehende Inseln
in einer ansonsten abstoßenden
. Ohne erkennbare Symmetrie verteilte anziehende Inseln
in einer ansonsten abstoßenden 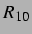 -
-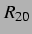 -Ebene.
-Ebene.
|
|
Die Sequenz für
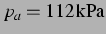 findet sich qualitativ auch in den nächsten Sequenzen
für höhere Anregungsdrücke wieder. So ist in Abbildung 4.28 für
findet sich qualitativ auch in den nächsten Sequenzen
für höhere Anregungsdrücke wieder. So ist in Abbildung 4.28 für  die gleiche Symmetrie wie in
Abbildung 4.25 zu erkennen. Es zeigt sich
jedoch, dass der obere Grenzruheradius der abstoßenden Bereiche wie auch bei
METTIN et al. zu niedrigeren Werten geht. Er liegt hier bei etwa
die gleiche Symmetrie wie in
Abbildung 4.25 zu erkennen. Es zeigt sich
jedoch, dass der obere Grenzruheradius der abstoßenden Bereiche wie auch bei
METTIN et al. zu niedrigeren Werten geht. Er liegt hier bei etwa 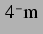 . In Abbildung 4.29
erkennt man ein gegenüber Abbildung 4.26 nur geringfügig verändertes Muster, und
in Abbildung 4.30 gibt es weniger
anziehende Bereiche als bei einem anregenden Schalldruck von
. In Abbildung 4.29
erkennt man ein gegenüber Abbildung 4.26 nur geringfügig verändertes Muster, und
in Abbildung 4.30 gibt es weniger
anziehende Bereiche als bei einem anregenden Schalldruck von
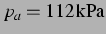 .
.
Abbildung: Sekundäre Bjerkneskraft aus der nichtlinearen
Simulation und ihr Vorzeichen bei  (
(
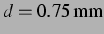 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
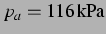 . Die obere Grenze der abstoßenden Bereiche ist mit
höherem Druck zu kleineren Ruheradien gewandert. Das ließ sich auch
in [25] beobachten.
. Die obere Grenze der abstoßenden Bereiche ist mit
höherem Druck zu kleineren Ruheradien gewandert. Das ließ sich auch
in [25] beobachten.
|
|
Abbildung 4.29: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  (
(
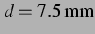 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
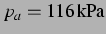 . Ein ähnliches Muster wie in Abbildung 4.26.
. Ein ähnliches Muster wie in Abbildung 4.26.
|
|
Abbildung: Sekundäre Bjerkneskraft aus der nichtlinearen
Simulation und ihr Vorzeichen bei  (
(
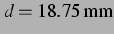 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
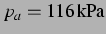 . Wieder große abstoßende Bereiche, mit
weniger anziehenden Inseln.
. Wieder große abstoßende Bereiche, mit
weniger anziehenden Inseln.
|
|
Bei einer weiteren Erhöhung der Anregung auf
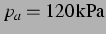 sinken die Ruheradien, die bei einem Delay von
sinken die Ruheradien, die bei einem Delay von  die
abstoßenden Bereiche nach oben begrenzen weiter auf nun etwa
die
abstoßenden Bereiche nach oben begrenzen weiter auf nun etwa 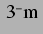 , und
die Felder sind schärfer begrenzt. Der höhere Druck bewirkt
gewissermaßen eine Bereinigung der Vorzeichenstrukturen, wie auch in
Abbildung 4.32 durch das weniger zerfurchte
Muster und in Abbildung 4.33 mit weniger
verteilten anziehenden Bereichen deutlich wird.
, und
die Felder sind schärfer begrenzt. Der höhere Druck bewirkt
gewissermaßen eine Bereinigung der Vorzeichenstrukturen, wie auch in
Abbildung 4.32 durch das weniger zerfurchte
Muster und in Abbildung 4.33 mit weniger
verteilten anziehenden Bereichen deutlich wird.
Abbildung: Sekundäre Bjerkneskraft aus der nichtlinearen
Simulation und ihr Vorzeichen bei  (
(
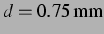 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
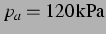 . Die obere Grenze der abstoßenden Bereiche ist auf
etwa
. Die obere Grenze der abstoßenden Bereiche ist auf
etwa 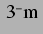 gesunken und ist schärfer begrenzt.
gesunken und ist schärfer begrenzt.
|
|
Abbildung 4.32: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  (
(
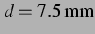 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
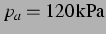 . Das Muster wirkt weniger zerfurcht. Der höhere
Druck bewirkt eine Bereinigung der Vorzeichenstrukturen.
. Das Muster wirkt weniger zerfurcht. Der höhere
Druck bewirkt eine Bereinigung der Vorzeichenstrukturen.
|
|
Abbildung: Sekundäre Bjerkneskraft aus der nichtlinearen
Simulation und ihr Vorzeichen bei  (
(
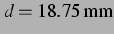 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
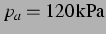 . Keine großartige Veränderung gegenüber
dem Bild bei
. Keine großartige Veränderung gegenüber
dem Bild bei
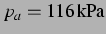 , abgesehen davon, dass die anziehenden Bereiche weniger
verstreut sind.
, abgesehen davon, dass die anziehenden Bereiche weniger
verstreut sind.
|
|
Die Tendenzen zu ,,aufgeräumteren`` Strukturen und kleineren oberen Grenzen
im Fall  setzen sich mit höheren Drücken weiter fort. Bei
setzen sich mit höheren Drücken weiter fort. Bei
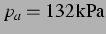 schließlich ist für
schließlich ist für  nur noch ein sehr
schmaler Streifen für Ruheradien kleiner als
nur noch ein sehr
schmaler Streifen für Ruheradien kleiner als 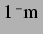 (teilweise
(teilweise 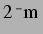 )
anziehend, und für
)
anziehend, und für  ebenfalls nur noch ein sehr kleiner Streifen bei sehr
kleinem Ruheradius der ersten Blase anziehend. Bei
ebenfalls nur noch ein sehr kleiner Streifen bei sehr
kleinem Ruheradius der ersten Blase anziehend. Bei  wird die dargestellte
wird die dargestellte 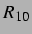 -
-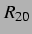 -Ebene
annähernd horizontal in der Mitte geteilt.
-Ebene
annähernd horizontal in der Mitte geteilt.
Abbildung 4.34: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  (
(
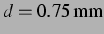 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
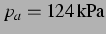 .
.
|
|
Abbildung 4.35: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  (
(
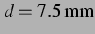 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
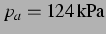 .
.
|
|
Abbildung 4.36: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  (
(
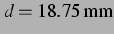 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
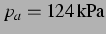 .
.
|
|
Abbildung 4.37: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  (
(
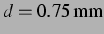 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
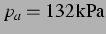 .
.
|
|
Abbildung 4.38: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  (
(
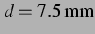 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
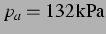 .
.
|
|
Abbildung 4.39: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  (
(
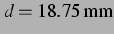 ) und für hohen Anregungsdruck:
) und für hohen Anregungsdruck:
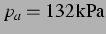 .
.
|
|
Es lassen sich also wie in [25]
beobachten, dass es bei hohen Drücken abstoßende Bereiche in der 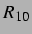 -
-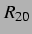 -Ebene
gibt, wenn eine der beiden Blasen klein ist, und dass die obere Grenze dieser
Bereiche für zunehmenden Anregungsdruck gegen kleinere Ruheradien geht. Im
Unterschied zu den Beobachtungen instantan gekoppelten Fall treten diese Bereiche
jedoch bei kleinem Delay bereits bei weitaus geringeren Drücken auf. Eine
weitere Entfernung der Blasen voneinander bewirkt eine massive Änderung der
Vorzeichenverteilung. Da die Abweichung vom instantan gekoppelten Blasenmodell bei
Delaywerten auftritt, die in einem Bereich liegen, wie er in der Strukturbildung
beobachtet wird, darf man den Einfluss des Delays auf die sekundären
Bjerkneskraft nicht vernachlässigen. Allen Ergebnissen ist gemeinsam, dass sie
die Invarianz der Vorzeichenverteilung der Indexvertauschung brechen. Das
schließt die Möglichkeit ein, dass die Delay-Kopplung für das
Auftreten der Streamer, auf denen sich die Blasen in das Zentrum der Struktur
bewegen, mitverantwortlich ist.
-Ebene
gibt, wenn eine der beiden Blasen klein ist, und dass die obere Grenze dieser
Bereiche für zunehmenden Anregungsdruck gegen kleinere Ruheradien geht. Im
Unterschied zu den Beobachtungen instantan gekoppelten Fall treten diese Bereiche
jedoch bei kleinem Delay bereits bei weitaus geringeren Drücken auf. Eine
weitere Entfernung der Blasen voneinander bewirkt eine massive Änderung der
Vorzeichenverteilung. Da die Abweichung vom instantan gekoppelten Blasenmodell bei
Delaywerten auftritt, die in einem Bereich liegen, wie er in der Strukturbildung
beobachtet wird, darf man den Einfluss des Delays auf die sekundären
Bjerkneskraft nicht vernachlässigen. Allen Ergebnissen ist gemeinsam, dass sie
die Invarianz der Vorzeichenverteilung der Indexvertauschung brechen. Das
schließt die Möglichkeit ein, dass die Delay-Kopplung für das
Auftreten der Streamer, auf denen sich die Blasen in das Zentrum der Struktur
bewegen, mitverantwortlich ist.




Nächste Seite: Ausgewählte
Trajektorien von Kavitationsblasen Aufwärts: Ergebnisse der numerischen Simulationen Vorherige
Seite: Sekundäre Bjerkneskraft bei
hohem Inhalt
Stefan Kamphausen 2003-07-17
![]() bei obigen
Anregungsdrücken und ansonsten identischen Parametern (s. Tabelle 2.1) der Bjerkneskoeffizient, der dort als
bei obigen
Anregungsdrücken und ansonsten identischen Parametern (s. Tabelle 2.1) der Bjerkneskoeffizient, der dort als![\includegraphics [width=8.5cm]{1_20/fb_100_1.12_ha.ps}](img425.png)
![\includegraphics [width=6.791cm]{1_20/fb_100_1.12_sig_ha.ps}](img426.png)
![\includegraphics [width=8.5cm]{1_20/fb_10_1.12_ha.ps}](img429.png)
![\includegraphics [width=6.791cm]{1_20/fb_10_1.12_sig_ha.ps}](img430.png)
![\includegraphics [width=8.5cm]{1_20/fb_4_1.12_ha.ps}](img431.png)
![\includegraphics [width=6.791cm]{1_20/fb_4_1.12_sig_ha.ps}](img432.png)
![]() findet sich qualitativ auch in den nächsten Sequenzen
für höhere Anregungsdrücke wieder. So ist in Abbildung 4.28 für
findet sich qualitativ auch in den nächsten Sequenzen
für höhere Anregungsdrücke wieder. So ist in Abbildung 4.28 für ![]() die gleiche Symmetrie wie in
Abbildung 4.25 zu erkennen. Es zeigt sich
jedoch, dass der obere Grenzruheradius der abstoßenden Bereiche wie auch bei
METTIN et al. zu niedrigeren Werten geht. Er liegt hier bei etwa
die gleiche Symmetrie wie in
Abbildung 4.25 zu erkennen. Es zeigt sich
jedoch, dass der obere Grenzruheradius der abstoßenden Bereiche wie auch bei
METTIN et al. zu niedrigeren Werten geht. Er liegt hier bei etwa ![]() . In Abbildung 4.29
erkennt man ein gegenüber Abbildung 4.26 nur geringfügig verändertes Muster, und
in Abbildung 4.30 gibt es weniger
anziehende Bereiche als bei einem anregenden Schalldruck von
. In Abbildung 4.29
erkennt man ein gegenüber Abbildung 4.26 nur geringfügig verändertes Muster, und
in Abbildung 4.30 gibt es weniger
anziehende Bereiche als bei einem anregenden Schalldruck von
![]() .
.![\includegraphics [width=8.5cm]{1_20/fb_100_1.16_ha.ps}](img434.png)
![\includegraphics [width=6.791cm]{1_20/fb_100_1.16_sig_ha.ps}](img435.png)
![\includegraphics [width=8.5cm]{1_20/fb_10_1.16_ha.ps}](img437.png)
![\includegraphics [width=6.791cm]{1_20/fb_10_1.16_sig_ha.ps}](img438.png)
![\includegraphics [width=8.5cm]{1_20/fb_4_1.16_ha.ps}](img439.png)
![\includegraphics [width=6.791cm]{1_20/fb_4_1.16_sig_ha.ps}](img440.png)
![]() sinken die Ruheradien, die bei einem Delay von
sinken die Ruheradien, die bei einem Delay von ![]() die
abstoßenden Bereiche nach oben begrenzen weiter auf nun etwa
die
abstoßenden Bereiche nach oben begrenzen weiter auf nun etwa ![]() , und
die Felder sind schärfer begrenzt. Der höhere Druck bewirkt
gewissermaßen eine Bereinigung der Vorzeichenstrukturen, wie auch in
Abbildung 4.32 durch das weniger zerfurchte
Muster und in Abbildung 4.33 mit weniger
verteilten anziehenden Bereichen deutlich wird.
, und
die Felder sind schärfer begrenzt. Der höhere Druck bewirkt
gewissermaßen eine Bereinigung der Vorzeichenstrukturen, wie auch in
Abbildung 4.32 durch das weniger zerfurchte
Muster und in Abbildung 4.33 mit weniger
verteilten anziehenden Bereichen deutlich wird.![\includegraphics [width=8.5cm]{1_20/fb_100_1.2_ha.ps}](img443.png)
![\includegraphics [width=6.791cm]{1_20/fb_100_1.2_sig_ha.ps}](img444.png)
![\includegraphics [width=8.5cm]{1_20/fb_10_1.2_ha.ps}](img445.png)
![\includegraphics [width=6.791cm]{1_20/fb_10_1.2_sig_ha.ps}](img446.png)
![\includegraphics [width=8.5cm]{1_20/fb_4_1.2_ha.ps}](img447.png)
![\includegraphics [width=6.791cm]{1_20/fb_4_1.2_sig_ha.ps}](img448.png)
![]() setzen sich mit höheren Drücken weiter fort. Bei
setzen sich mit höheren Drücken weiter fort. Bei
![]() schließlich ist für
schließlich ist für ![]() nur noch ein sehr
schmaler Streifen für Ruheradien kleiner als
nur noch ein sehr
schmaler Streifen für Ruheradien kleiner als ![]() (teilweise
(teilweise ![]() )
anziehend, und für
)
anziehend, und für ![]() ebenfalls nur noch ein sehr kleiner Streifen bei sehr
kleinem Ruheradius der ersten Blase anziehend. Bei
ebenfalls nur noch ein sehr kleiner Streifen bei sehr
kleinem Ruheradius der ersten Blase anziehend. Bei ![]() wird die dargestellte
wird die dargestellte ![]() -
-![]() -Ebene
annähernd horizontal in der Mitte geteilt.
-Ebene
annähernd horizontal in der Mitte geteilt.![\includegraphics [width=8.5cm]{1_20/fb_100_1.24_ha.ps}](img450.png)
![\includegraphics [width=6.791cm]{1_20/fb_100_1.24_sig_ha.ps}](img451.png)
![\includegraphics [width=8.5cm]{1_20/fb_10_1.24_ha.ps}](img453.png)
![\includegraphics [width=6.791cm]{1_20/fb_10_1.24_sig_ha.ps}](img454.png)
![\includegraphics [width=8.5cm]{1_20/fb_4_1.24_ha.ps}](img455.png)
![\includegraphics [width=6.791cm]{1_20/fb_4_1.24_sig_ha.ps}](img456.png)
![\includegraphics [width=8.5cm]{1_20/fb_100_1.32_ha.ps}](img457.png)
![\includegraphics [width=6.791cm]{1_20/fb_100_1.32_sig_ha.ps}](img458.png)
![\includegraphics [width=8.5cm]{1_20/fb_10_1.32_ha.ps}](img459.png)
![\includegraphics [width=6.791cm]{1_20/fb_10_1.32_sig_ha.ps}](img460.png)
![\includegraphics [width=8.5cm]{1_20/fb_4_1.32_ha.ps}](img461.png)
![\includegraphics [width=6.791cm]{1_20/fb_4_1.32_sig_ha.ps}](img462.png)
![]() -
-![]() -Ebene
gibt, wenn eine der beiden Blasen klein ist, und dass die obere Grenze dieser
Bereiche für zunehmenden Anregungsdruck gegen kleinere Ruheradien geht. Im
Unterschied zu den Beobachtungen instantan gekoppelten Fall treten diese Bereiche
jedoch bei kleinem Delay bereits bei weitaus geringeren Drücken auf. Eine
weitere Entfernung der Blasen voneinander bewirkt eine massive Änderung der
Vorzeichenverteilung. Da die Abweichung vom instantan gekoppelten Blasenmodell bei
Delaywerten auftritt, die in einem Bereich liegen, wie er in der Strukturbildung
beobachtet wird, darf man den Einfluss des Delays auf die sekundären
Bjerkneskraft nicht vernachlässigen. Allen Ergebnissen ist gemeinsam, dass sie
die Invarianz der Vorzeichenverteilung der Indexvertauschung brechen. Das
schließt die Möglichkeit ein, dass die Delay-Kopplung für das
Auftreten der Streamer, auf denen sich die Blasen in das Zentrum der Struktur
bewegen, mitverantwortlich ist.
-Ebene
gibt, wenn eine der beiden Blasen klein ist, und dass die obere Grenze dieser
Bereiche für zunehmenden Anregungsdruck gegen kleinere Ruheradien geht. Im
Unterschied zu den Beobachtungen instantan gekoppelten Fall treten diese Bereiche
jedoch bei kleinem Delay bereits bei weitaus geringeren Drücken auf. Eine
weitere Entfernung der Blasen voneinander bewirkt eine massive Änderung der
Vorzeichenverteilung. Da die Abweichung vom instantan gekoppelten Blasenmodell bei
Delaywerten auftritt, die in einem Bereich liegen, wie er in der Strukturbildung
beobachtet wird, darf man den Einfluss des Delays auf die sekundären
Bjerkneskraft nicht vernachlässigen. Allen Ergebnissen ist gemeinsam, dass sie
die Invarianz der Vorzeichenverteilung der Indexvertauschung brechen. Das
schließt die Möglichkeit ein, dass die Delay-Kopplung für das
Auftreten der Streamer, auf denen sich die Blasen in das Zentrum der Struktur
bewegen, mitverantwortlich ist.