



Nächste Seite: Sekundäre
Bjerkneskraft bei hohem Aufwärts: Ergebnisse der numerischen Simulationen Vorherige Seite: Ergebnisse der numerischen Simulationen
Inhalt
Sekundäre Bjerkneskraft bei geringen Drücken
Bei geringen Drücken 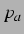 von
von 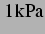 und
und  erwartet man ein ähnliches
Ergebnis wie von der linearisierten Keller-Miksis-Gleichung, da die
Nichtlinearitäten hier noch nicht so stark zum Tragen kommen.
erwartet man ein ähnliches
Ergebnis wie von der linearisierten Keller-Miksis-Gleichung, da die
Nichtlinearitäten hier noch nicht so stark zum Tragen kommen.
Abbildung: Sekundäre Bjerkneskraft aus der nichtlinearen
Simulation und ihr Vorzeichen bei  , entspricht einem Blasenabstand
von
, entspricht einem Blasenabstand
von
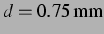 . Der Schalldruck der Anregung beträgt
. Der Schalldruck der Anregung beträgt
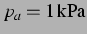 . Anziehende Kräfte für gleich große
Blasen, aber sonst bei großen Ruheradien keine Anziehung entgegen den
Ergebnissen der linearen Modelle (vgl. mit Abb. 3.1 und Abb. 3.13).
. Anziehende Kräfte für gleich große
Blasen, aber sonst bei großen Ruheradien keine Anziehung entgegen den
Ergebnissen der linearen Modelle (vgl. mit Abb. 3.1 und Abb. 3.13).
|
|
Die erste Serie von Abbildungen 4.1
bis 4.8 zeigt wie auch schon in
Kapitel 3 die diesmal jedoch nach dem
nichtlinearen Modell berechnete sekundäre Bjerkneskraft 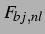 sowie ihr
Vorzeichen für
sowie ihr
Vorzeichen für  ,
, 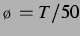 ,
,  ,
, 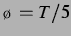 ,
, 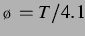 ,
,  ,
, 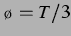 und
und
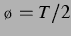 zunächst bei einem anregenden Schalldruck von
zunächst bei einem anregenden Schalldruck von 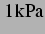 in der
in der
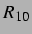 -
-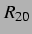 -Ebene.
-Ebene.
Ein Problem der numerischen Simulation liegt bei Blasenparametern, die zu einer
chaotischen Lösung führen oder aber eine sehr lange Einschwingphase haben,
bis sich eine stabile Schwingung ergibt. Das Programm berücksichtigte dabei
Lösungen mit einer Periodizität 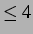 . In solchen Fällen ist es schwierig,
die zeitliche Mittelung aus Gleichung (2.11) durchzuführen. Unter Umständen ist die
sekundäre Bjerkneskraft in einem Intervall
. In solchen Fällen ist es schwierig,
die zeitliche Mittelung aus Gleichung (2.11) durchzuführen. Unter Umständen ist die
sekundäre Bjerkneskraft in einem Intervall
![$[t_1=N\cdot T;t_2=(N+1)\cdot T]$](img354.png) eine andere als in dem darauffolgenden
eine andere als in dem darauffolgenden 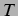 -Intervall. Daher ist zur Bewertung der Ergebnisse meist auch ein Blick auf die
Einschwingzeiten notwendig. Die Ergebnisse sollten sich mit längeren
Einschwingphasen nicht mehr substanziell ändern, um als ordentlich angesehen
werden zu können.
-Intervall. Daher ist zur Bewertung der Ergebnisse meist auch ein Blick auf die
Einschwingzeiten notwendig. Die Ergebnisse sollten sich mit längeren
Einschwingphasen nicht mehr substanziell ändern, um als ordentlich angesehen
werden zu können.
Abbildung 4.1 zeigt die Situation für
 . Die auffälligste Veränderung zu den Ergebnissen der
linearen Theorie ist, dass sich zwar Blasen mit gleichem Ruheradius auch weiterhin
gegenseitig anziehen, sich jedoch in bei großen Ruheradien abstoßen,
sobald sie sich unterscheiden. Dies steht im Gegensatz zu den sekundären
Bjerkneskräften, die sich aus der Linearisierung der Keller-Miksis-Gleichung
ergeben haben. Dort stoßen sich gleich große Blasen erst bei einem Delay
. Die auffälligste Veränderung zu den Ergebnissen der
linearen Theorie ist, dass sich zwar Blasen mit gleichem Ruheradius auch weiterhin
gegenseitig anziehen, sich jedoch in bei großen Ruheradien abstoßen,
sobald sie sich unterscheiden. Dies steht im Gegensatz zu den sekundären
Bjerkneskräften, die sich aus der Linearisierung der Keller-Miksis-Gleichung
ergeben haben. Dort stoßen sich gleich große Blasen erst bei einem Delay
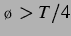 gegenseitig ab. Dieses spricht dafür, dass die Linearisierung
der Keller-Miksis-Gleichung in dem Fall sehr kleinen Delays nicht gerechtfertigt ist.
Einige Beobachtungen finden sich auch hier wieder. So bleibt die Verlagerung der
Extremwerte der sekundären Bjerkneskraft sowie die Verschiebung der
vorzeichenwechselnden Ruheradien zu höheren Werten ist zu erkennen.
gegenseitig ab. Dieses spricht dafür, dass die Linearisierung
der Keller-Miksis-Gleichung in dem Fall sehr kleinen Delays nicht gerechtfertigt ist.
Einige Beobachtungen finden sich auch hier wieder. So bleibt die Verlagerung der
Extremwerte der sekundären Bjerkneskraft sowie die Verschiebung der
vorzeichenwechselnden Ruheradien zu höheren Werten ist zu erkennen.
Abbildung 4.2: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei 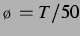 , entspricht einem
Blasenabstand von
, entspricht einem
Blasenabstand von
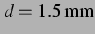 . Anregung mit
. Anregung mit
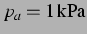 . Die Verschiebung der Ruheradien, bei denen das Vorzeichen
wechselt, finden sich auch hier wieder wie in der linearen Näherung mit
Kopplung (vgl. Abb. 3.14).
. Die Verschiebung der Ruheradien, bei denen das Vorzeichen
wechselt, finden sich auch hier wieder wie in der linearen Näherung mit
Kopplung (vgl. Abb. 3.14).
|
|
Bei 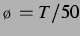 in Abbildung 4.2 findet
sich dagegen wieder das gewohnte Bild wie in der entsprechenden Abbildung 3.14. Die Grenzen der ausgezeichneten Flächen
sind etwas ,,angeknabbert``, und durch eine hier benutzte Interpolation (es wurde nur
ein Drittel der Daten berechnet, die beim linearisierten Modell vorhanden waren)
etwas verschwommen. Am Rand der dargestellten Ebene lässt sich nicht mehr
interpolieren, was dazu führt, dass dort die Felder gleichen Vorzeichens scharf
begrenzt sind. Dies fällt nur bei genauem Hinsehen auf. Das Ergebnis stimmt gut
mit dem aus Abbildung 3.14 überein bis
auf einen kleinen Bereich in der Mitte, in dem eine (zur Winkelhalbierenden
symmetrische) Unregelmäßigkeit sichtbar wird. Auch die Verschiebung der
vorzeichenwechselnden Ruheradien zu höheren Werten gegenüber dem nicht
gekoppelten Fall wird hier durch das volle Modell bestätigt, sowie die
Entwicklung bei größerem Delay, die Annäherung an die nicht
gekoppelten Werte in der Nähe von
in Abbildung 4.2 findet
sich dagegen wieder das gewohnte Bild wie in der entsprechenden Abbildung 3.14. Die Grenzen der ausgezeichneten Flächen
sind etwas ,,angeknabbert``, und durch eine hier benutzte Interpolation (es wurde nur
ein Drittel der Daten berechnet, die beim linearisierten Modell vorhanden waren)
etwas verschwommen. Am Rand der dargestellten Ebene lässt sich nicht mehr
interpolieren, was dazu führt, dass dort die Felder gleichen Vorzeichens scharf
begrenzt sind. Dies fällt nur bei genauem Hinsehen auf. Das Ergebnis stimmt gut
mit dem aus Abbildung 3.14 überein bis
auf einen kleinen Bereich in der Mitte, in dem eine (zur Winkelhalbierenden
symmetrische) Unregelmäßigkeit sichtbar wird. Auch die Verschiebung der
vorzeichenwechselnden Ruheradien zu höheren Werten gegenüber dem nicht
gekoppelten Fall wird hier durch das volle Modell bestätigt, sowie die
Entwicklung bei größerem Delay, die Annäherung an die nicht
gekoppelten Werte in der Nähe von
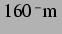 , bei
, bei  in Abbildung 4.3.
in Abbildung 4.3.
Ein weiterer wesentlicher Unterschied in der linearen Näherung zwischen dem
gekoppelten und dem ungekoppelten Fall ist das spätere Auseinanderdriften der
abstoßenden Bereiche bei 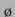 -Werten näher an
-Werten näher an 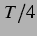 . Auch dieses findet sich im
nichtlinearen Modell bestätigt, wie man durch Vergleich der Abbildung 4.3 mit den Abbildungen aus der linearen
Näherung 3.2 (ungekoppelt)
und 3.15 (gekoppelt) feststellt.
. Auch dieses findet sich im
nichtlinearen Modell bestätigt, wie man durch Vergleich der Abbildung 4.3 mit den Abbildungen aus der linearen
Näherung 3.2 (ungekoppelt)
und 3.15 (gekoppelt) feststellt.
Abbildung 4.3: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  , entspricht
einem Blasenabstand von
, entspricht
einem Blasenabstand von
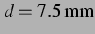 , und einem anregenden Schalldruck
, und einem anregenden Schalldruck
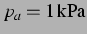 . Die Vorzeichenwechsel bewegen sich genau wie im
linearisierten Modell mit Kopplung zu kleineren Ruheradien (vgl. Abb. 3.2 u. Abb. 3.15).
. Die Vorzeichenwechsel bewegen sich genau wie im
linearisierten Modell mit Kopplung zu kleineren Ruheradien (vgl. Abb. 3.2 u. Abb. 3.15).
|
|
Abbildung 4.4: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei 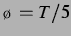 , entspricht einem
Blasenabstand von
, entspricht einem
Blasenabstand von 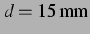 , und einem anregenden Schalldruck
, und einem anregenden Schalldruck
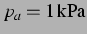 . Wie im Fall der delay-gekoppelten, harmonisch
schwingenden Blasen in Abb. 3.16
entfernen sich die Flächen gleichen Vorzeichens langsamer voneinander als
in Abb. 3.3.
. Wie im Fall der delay-gekoppelten, harmonisch
schwingenden Blasen in Abb. 3.16
entfernen sich die Flächen gleichen Vorzeichens langsamer voneinander als
in Abb. 3.3.
|
|
In den folgenden Abbildungen, die die Situation für 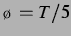 bis
bis 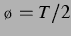 zeigen, erkennt man das aus der linearen Theorie vorhergesagte Verhalten wieder.
Lediglich einige kleine Unregelmäßigkeiten sind in den Bildern zu sehen,
die zumeist den beginnenden Einfluss der Nichtlinearitäten wiederspiegeln. Sie
ließen sich auch durch eine längere Einschwingphase nicht bereinigen, so
dass man davon ausgehen darf, dass die weiterhin sichtbaren Effekte durch die
Nichtlinearität hervorgerufen werden. Sie ändern jedoch nichts an der
groben Struktur der Muster. Wie gewohnt erhält man für
zeigen, erkennt man das aus der linearen Theorie vorhergesagte Verhalten wieder.
Lediglich einige kleine Unregelmäßigkeiten sind in den Bildern zu sehen,
die zumeist den beginnenden Einfluss der Nichtlinearitäten wiederspiegeln. Sie
ließen sich auch durch eine längere Einschwingphase nicht bereinigen, so
dass man davon ausgehen darf, dass die weiterhin sichtbaren Effekte durch die
Nichtlinearität hervorgerufen werden. Sie ändern jedoch nichts an der
groben Struktur der Muster. Wie gewohnt erhält man für  in
Abbildung 4.6 die durch die
Winkelhalbierende geteilte
in
Abbildung 4.6 die durch die
Winkelhalbierende geteilte 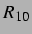 -
-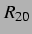 -Ebene (hier mit zusätzlichen Mustern in der Nähe
des Vorzeichenwechsels) und bei
-Ebene (hier mit zusätzlichen Mustern in der Nähe
des Vorzeichenwechsels) und bei 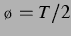 die umgekehrten Vorzeichen.
die umgekehrten Vorzeichen.
Auch die mit zunehmendem Abstand schwächer werdende Kopplung, die sich in der
Geometrie des Bjerkneskraftgebirges als eine Verlagerung der Spitzen zum zentralen
Punkt und eine Dominanz der ,,Resonanzkämme`` wiederspiegelt, ist hier zu
beobachten. Bei  liegen die Gipfel noch bei hohen Ruheradien, bei
liegen die Gipfel noch bei hohen Ruheradien, bei  bereits in der Nähe des Punktes, an dem beide Blasen einen Ruheradius beim
Resonanzradius haben, wobei von außen die charakteristischen Kämme
heranwachsen. Und bei allen größeren Abständen liegen die Extremwerte
in der Mitte.
bereits in der Nähe des Punktes, an dem beide Blasen einen Ruheradius beim
Resonanzradius haben, wobei von außen die charakteristischen Kämme
heranwachsen. Und bei allen größeren Abständen liegen die Extremwerte
in der Mitte.
Abbildung 4.5: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei 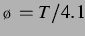 , entspricht
einem Blasenabstand von
, entspricht
einem Blasenabstand von
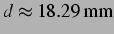 . Die Anregung erfolgte in dieser Serie mit
. Die Anregung erfolgte in dieser Serie mit
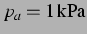 (vgl. Abb. 3.4
und Abb. 3.17).
(vgl. Abb. 3.4
und Abb. 3.17).
|
|
Abbildung 4.6: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  , entspricht einem
Blasenabstand von
, entspricht einem
Blasenabstand von
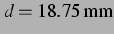 , und dem anregenden Schalldruck
, und dem anregenden Schalldruck
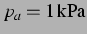 . Auch hier findet sich die ,,maximal gebrochene``
Symmetrie (im Sinne von Abschnitt 3.1.2). Nichtlinearitäten überlagern
noch ein weiteres, feineres Muster über die Winkelhalbierende aus der
linearen Theorie (vgl. Abb. 3.5 und
Abb. 3.18.
. Auch hier findet sich die ,,maximal gebrochene``
Symmetrie (im Sinne von Abschnitt 3.1.2). Nichtlinearitäten überlagern
noch ein weiteres, feineres Muster über die Winkelhalbierende aus der
linearen Theorie (vgl. Abb. 3.5 und
Abb. 3.18.
|
|
Abbildung 4.7: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei 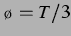 , entspricht einem
Blasenabstand von
, entspricht einem
Blasenabstand von 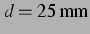 , und dem anregenden Schalldruck
, und dem anregenden Schalldruck
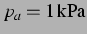 . Umdrehen der Vorzeichen für
. Umdrehen der Vorzeichen für 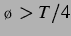 wie auch
in den Abbildungen 3.7 und 3.19.
wie auch
in den Abbildungen 3.7 und 3.19.
|
|
Abbildung: Sekundäre Bjerkneskraft aus der nichtlinearen
Simulation und ihr Vorzeichen bei 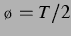 , entspricht einem Blasenabstand
von
, entspricht einem Blasenabstand
von
 , und dem anregenden Schalldruck
, und dem anregenden Schalldruck
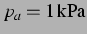 . Für größere
. Für größere 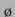 wiederholt sich die
Serie der Vorzeichenmuster mit der Periodenlänge
wiederholt sich die
Serie der Vorzeichenmuster mit der Periodenlänge 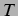 wie in Abb. 3.8 (vgl. auch Abb. 3.20).
wie in Abb. 3.8 (vgl. auch Abb. 3.20).
|
|
Die zweite Serie in diesem Abschnitt zeigt die Situation für die
üblichen 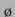 -Werte bei einem anregenden Schallfeld von
-Werte bei einem anregenden Schallfeld von  . Es wird also der
Fall betrachtet, bei dem die sekundären Bjerkneskräfte in der linearen
Näherung in Kapitel 3 dargestellt wurden.
Dieser Anregungsdruck liegt bei einem Druck, der die Linearisierbarkeit nicht mehr
unbedingt gewährleistet. Damit ist die Möglichkeit gegeben, die Grenzen der
Gültigkeit abzuschätzen. Es wurde gezeigt, dass für einen anregenden
Schalldruck von
. Es wird also der
Fall betrachtet, bei dem die sekundären Bjerkneskräfte in der linearen
Näherung in Kapitel 3 dargestellt wurden.
Dieser Anregungsdruck liegt bei einem Druck, der die Linearisierbarkeit nicht mehr
unbedingt gewährleistet. Damit ist die Möglichkeit gegeben, die Grenzen der
Gültigkeit abzuschätzen. Es wurde gezeigt, dass für einen anregenden
Schalldruck von 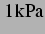 , der im linearisierten Modell qualitativ die
gleichen Ergebnisse liefert wie ein höherer, da die Amplitude der Schwingung ja
linear (vgl. Gl. (3.11) und Gl. (3.25)) und somit die sekundäre Bjerkneskraft
quadratisch mit
, der im linearisierten Modell qualitativ die
gleichen Ergebnisse liefert wie ein höherer, da die Amplitude der Schwingung ja
linear (vgl. Gl. (3.11) und Gl. (3.25)) und somit die sekundäre Bjerkneskraft
quadratisch mit 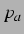 skaliert (vgl. Gl. (3.17),
in der der Druck nur in den Amplituden beider Blasen je einmal auftaucht), die
Ergebnisse aus der Linearisierung gut wiedergefunden werden konnten. Nun soll
untersucht werden, ob sich das bei einem höheren Schalldruck immer noch ergibt.
Die gezeigten Abbildungen sind also einerseits mit ihren Pendants aus der ersten
Serie dieses Abschnitts zu vergleichen, um den Effekt, den der höhere
Schalldruck bewirkt, zu studieren, andererseits mit denen aus Abschnitt 3.2.2, um den Einfluss der Nichtlinearitäten zu
betrachten.
skaliert (vgl. Gl. (3.17),
in der der Druck nur in den Amplituden beider Blasen je einmal auftaucht), die
Ergebnisse aus der Linearisierung gut wiedergefunden werden konnten. Nun soll
untersucht werden, ob sich das bei einem höheren Schalldruck immer noch ergibt.
Die gezeigten Abbildungen sind also einerseits mit ihren Pendants aus der ersten
Serie dieses Abschnitts zu vergleichen, um den Effekt, den der höhere
Schalldruck bewirkt, zu studieren, andererseits mit denen aus Abschnitt 3.2.2, um den Einfluss der Nichtlinearitäten zu
betrachten.
Abbildung: Sekundäre Bjerkneskraft aus der nichtlinearen
Simulation und ihr Vorzeichen bei  , entspricht einem Blasenabstand
von
, entspricht einem Blasenabstand
von
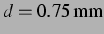 , und bei einem anregenden Schalldruck von
, und bei einem anregenden Schalldruck von
 . Es lassen sich die Ruheradien ablesen, bei denen sich
das Vorzeichen der Kraft umkehrt. Diese liegen bei dem durch die lineare
Theorie mit Kopplung bestimmten Wert: etwa
. Es lassen sich die Ruheradien ablesen, bei denen sich
das Vorzeichen der Kraft umkehrt. Diese liegen bei dem durch die lineare
Theorie mit Kopplung bestimmten Wert: etwa
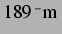 (vgl. Abb. 3.13). Für gleich große Ruheradien
wirkt die sekundäre Bjerkneskraft immer anziehend, aber den
abstoßenden Bereich der linearen Modelle für große Ruheradien
findet man nicht mehr (vgl. auch Abb. 3.1 und Abb. 4.1).
(vgl. Abb. 3.13). Für gleich große Ruheradien
wirkt die sekundäre Bjerkneskraft immer anziehend, aber den
abstoßenden Bereich der linearen Modelle für große Ruheradien
findet man nicht mehr (vgl. auch Abb. 3.1 und Abb. 4.1).
|
|
Wie schon bei der ersten Serie ist das Ergebnis für sehr kleines  erstaunlich, da die Verteilung der Vorzeichen so von der linearen Näherung
abweicht, dass die Linearisierbarkeit des Problems hier nicht gerechtfertigt scheint.
Die Form stimmt jedoch mit der aus Abbildung 4.1 sehr gut überein, wobei allerdings die
Größendordnung der Kraft in einem Bereich bei sehr großen Ruheradien
extrem zugenommen hat. Dabei gilt es zu beachten, dass sich die Blasen bei solchen
Ruheradien auf solche Werte aufziehen, dass sie sich beinahe berühren. Somit
darf keine sphärische Form mehr angenommen werden, was sowohl im
Keller-Miksis-Modell als auch bei der Berechnung der sekundären Bjerkneskraft
vorrausgesetzt wurde. Es wurden bei diesen Parametern auch Blasenpaare gefunden, die
sich gegenseitig extrem aufschaukeln und somit für die starken Kräfte in
diesem Modell verantwortlich sind. Die Lage der Vorzeichenwechsel stimmt dagegen
recht gut mit denen aus Abbildung 3.13
überein (etwa
erstaunlich, da die Verteilung der Vorzeichen so von der linearen Näherung
abweicht, dass die Linearisierbarkeit des Problems hier nicht gerechtfertigt scheint.
Die Form stimmt jedoch mit der aus Abbildung 4.1 sehr gut überein, wobei allerdings die
Größendordnung der Kraft in einem Bereich bei sehr großen Ruheradien
extrem zugenommen hat. Dabei gilt es zu beachten, dass sich die Blasen bei solchen
Ruheradien auf solche Werte aufziehen, dass sie sich beinahe berühren. Somit
darf keine sphärische Form mehr angenommen werden, was sowohl im
Keller-Miksis-Modell als auch bei der Berechnung der sekundären Bjerkneskraft
vorrausgesetzt wurde. Es wurden bei diesen Parametern auch Blasenpaare gefunden, die
sich gegenseitig extrem aufschaukeln und somit für die starken Kräfte in
diesem Modell verantwortlich sind. Die Lage der Vorzeichenwechsel stimmt dagegen
recht gut mit denen aus Abbildung 3.13
überein (etwa
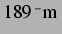 ). Sie hat sich durch den höheren Druck gegenüber der
ersten Serie in diesem Abschnitt nicht verändert (vgl. Abb. 4.1).
). Sie hat sich durch den höheren Druck gegenüber der
ersten Serie in diesem Abschnitt nicht verändert (vgl. Abb. 4.1).
Abbildung 4.10: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei 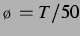 , entspricht einem
Blasenabstand von
, entspricht einem
Blasenabstand von
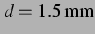 , und bei einem anregenden Schalldruck von
, und bei einem anregenden Schalldruck von
 . Bei diesem Schalldruck findet der Vorzeichenwechsel
bei niedrigeren Ruheradien statt, als das gekoppelte linearisierte Modell
vorhersagt (vgl. Abb. 3.14),
während die Ränder der Flächen gegenüber Abb. 4.2 als Folge des höheren Drucks weiter
,,ausfransen``. Das nichtlineare Verhalten der Blasen wird auch an dem Knick im
Gebirgsplot sichtbar (überhängende Resonanzkurven). S. auch
Abb. 4.2.
. Bei diesem Schalldruck findet der Vorzeichenwechsel
bei niedrigeren Ruheradien statt, als das gekoppelte linearisierte Modell
vorhersagt (vgl. Abb. 3.14),
während die Ränder der Flächen gegenüber Abb. 4.2 als Folge des höheren Drucks weiter
,,ausfransen``. Das nichtlineare Verhalten der Blasen wird auch an dem Knick im
Gebirgsplot sichtbar (überhängende Resonanzkurven). S. auch
Abb. 4.2.
|
|
In Abbildung 4.10 liegen die Ruheradien,
bei denen sich das Vorzeichen der sekundären Bjerkneskraft umkehrt bei
niedrigeren Werten, als es das lineare Modell mit Kopplung angibt. Das ist insofern
bemerkenswert als sich dieser Trend fortsetzt. Für  liegen diese Werte
sogar deutlich unter denen aus Abschnitt 3.2.2: unter
liegen diese Werte
sogar deutlich unter denen aus Abschnitt 3.2.2: unter
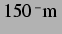 gegenüber mehr als
gegenüber mehr als
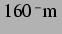 . Dies ist ein Anzeichen für das Verlassen der linearen
Näherung bei einem anregenden Schalldruck von
. Dies ist ein Anzeichen für das Verlassen der linearen
Näherung bei einem anregenden Schalldruck von  . Hinzu kommt, dass der
Betrag der Kraft durchgehend höher ist. Wie bereits erwähnt kann der Betrag
um Größenordnungen zunehmen, wenn die Blasenschwingung die lineare
Domäne verlässt. Im Gebirgsplot der sekundären Bjerkneskraft in
Abbildung 4.10 fällt zudem der starke
Knick auf, der in Resonanzkurven (und die sekundäre Bjerkneskraft folgt diesen
ja in weiten Teilen; s. Abschnitt 3.2.1)
ein Zeichen für das Anwachsen einer Nichtlinearität ist. Genaugenommen
hängen die Resonanzkurven hier über und es gibt zwei verschiedene stabile
Lösungen (Hysterese; s. [21]).
. Hinzu kommt, dass der
Betrag der Kraft durchgehend höher ist. Wie bereits erwähnt kann der Betrag
um Größenordnungen zunehmen, wenn die Blasenschwingung die lineare
Domäne verlässt. Im Gebirgsplot der sekundären Bjerkneskraft in
Abbildung 4.10 fällt zudem der starke
Knick auf, der in Resonanzkurven (und die sekundäre Bjerkneskraft folgt diesen
ja in weiten Teilen; s. Abschnitt 3.2.1)
ein Zeichen für das Anwachsen einer Nichtlinearität ist. Genaugenommen
hängen die Resonanzkurven hier über und es gibt zwei verschiedene stabile
Lösungen (Hysterese; s. [21]).
Abbildung 4.11: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei  , entspricht
einem Blasenabstand von
, entspricht
einem Blasenabstand von
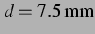 , und bei einem anregenden Schalldruck von
, und bei einem anregenden Schalldruck von
 . Die Vorzeichenwechsel liegen bei deutlich niedrigeren
Ruheradien als in der linearen Näherung, denen bei einem anregenden
Schalldruck von
. Die Vorzeichenwechsel liegen bei deutlich niedrigeren
Ruheradien als in der linearen Näherung, denen bei einem anregenden
Schalldruck von
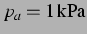 im nichtlinearen Modell noch gut entsprochen wurde (vgl.
mit Abb. 3.2, Abb. 3.15 und Abb. 4.3)
im nichtlinearen Modell noch gut entsprochen wurde (vgl.
mit Abb. 3.2, Abb. 3.15 und Abb. 4.3)
|
|
Abbildung: Sekundäre Bjerkneskraft aus der nichtlinearen
Simulation und ihr Vorzeichen bei 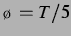 , entspricht einem Blasenabstand
von
, entspricht einem Blasenabstand
von 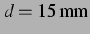 , und
, und
 . Die Größenordnung der sekundären
Bjerkneskraft stimmt gut mit der linearen Näherung überein, die
Vorzeichenwechsel liegen jedoch wie in den Fällen
. Die Größenordnung der sekundären
Bjerkneskraft stimmt gut mit der linearen Näherung überein, die
Vorzeichenwechsel liegen jedoch wie in den Fällen 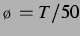 bei
niedrigeren Ruheradien. Die Geometrie der Vorzeichenverteilung bleibt weiterhin
gut erhalten. (Vgl. Abb. 3.3,
Abb. 3.16 und Abb. 4.4)
bei
niedrigeren Ruheradien. Die Geometrie der Vorzeichenverteilung bleibt weiterhin
gut erhalten. (Vgl. Abb. 3.3,
Abb. 3.16 und Abb. 4.4)
|
|
Abbildung 4.11 bei  zeigt
wieder die gewohnte Geometrie der Vorzeichenverteilung, bei allerdings kleineren
vorzeichenwechselnden Ruheradien. Die nichtlinearen Effekte sind hier nicht
ausschlaggebend. Gleiches gilt für Abbildung 4.12 bei
zeigt
wieder die gewohnte Geometrie der Vorzeichenverteilung, bei allerdings kleineren
vorzeichenwechselnden Ruheradien. Die nichtlinearen Effekte sind hier nicht
ausschlaggebend. Gleiches gilt für Abbildung 4.12 bei 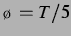 und Abbildung 4.13 bei
und Abbildung 4.13 bei 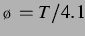 .
.
Abbildung 4.13: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei 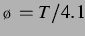 , entspricht
einem Blasenabstand von
, entspricht
einem Blasenabstand von
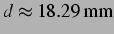 , und
, und
 . Diese Abbildung stimmt mit dem linearisierten
gekoppelten Modell in Abb. 3.17 in
bemerkenswerter Weise überein. Vgl. auch Abb. 3.4 und Abb. 4.5
. Diese Abbildung stimmt mit dem linearisierten
gekoppelten Modell in Abb. 3.17 in
bemerkenswerter Weise überein. Vgl. auch Abb. 3.4 und Abb. 4.5
|
|
Bemerkenswert ist weiterhin die sehr gute Übereinstimmung für 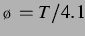 ,
also in einem Bereich, in dem sich die Vorzeichenmuster sehr schnell ändern, mit
der Abbildung 3.17 aus Abschnitt 3.2.2.
,
also in einem Bereich, in dem sich die Vorzeichenmuster sehr schnell ändern, mit
der Abbildung 3.17 aus Abschnitt 3.2.2.
Der Fall  , der in Abbildung 4.14
dargestellt ist, offenbart dann wieder eine Abweichung vom Ergebnis der linearen
Näherung. Bei Ruheradien zwischen
, der in Abbildung 4.14
dargestellt ist, offenbart dann wieder eine Abweichung vom Ergebnis der linearen
Näherung. Bei Ruheradien zwischen
 und
und
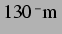 biegt die Grenze der Flächen gleichen Vorzeichens ab und
verlässt die Winkelhalbierende. Hier lassen sich nun auch Blasen finden, die
sich bei gleichem Ruheradius gegenseitig abstoßen.
biegt die Grenze der Flächen gleichen Vorzeichens ab und
verlässt die Winkelhalbierende. Hier lassen sich nun auch Blasen finden, die
sich bei gleichem Ruheradius gegenseitig abstoßen.
Abbildung: Sekundäre Bjerkneskraft aus der nichtlinearen
Simulation und ihr Vorzeichen bei  , entspricht einem Blasenabstand
von
, entspricht einem Blasenabstand
von
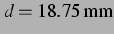 , und
, und
 . Die Trennlinie biegt von der Winkelhalbierenden ab,
so dass sich gleich große Blaasenpaare finden lassen, die sich
gegenseitig abstoßen. Vgl. mit Abb. 3.16, Abb. 3.18 und Abb. 4.6
. Die Trennlinie biegt von der Winkelhalbierenden ab,
so dass sich gleich große Blaasenpaare finden lassen, die sich
gegenseitig abstoßen. Vgl. mit Abb. 3.16, Abb. 3.18 und Abb. 4.6
|
|
Abbildung 4.15: sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei 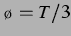 , entspricht einem
Blasenabstand von
, entspricht einem
Blasenabstand von 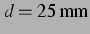 , und
, und
 . Auch hier drehen sich die Vorzeichen für
. Auch hier drehen sich die Vorzeichen für 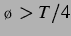 um, wie in Abb. 3.7, Abb. 3.19 und Abb. 4.7.
um, wie in Abb. 3.7, Abb. 3.19 und Abb. 4.7.
|
|
Die Abbildungen 4.15 und 4.16 zeigen dann wieder das erwartete Bild mit zu
kleineren Ruheradien verschobenen Vorzeichenwechseln bei umgedrehtem Vorzeichen
gegenüber der Verteilung für sehr kleines Delay.
Abbildung 4.16: Sekundäre Bjerkneskraft aus der
nichtlinearen Simulation und ihr Vorzeichen bei 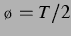 , entspricht einem
Blasenabstand von
, entspricht einem
Blasenabstand von
 , und
, und
 . Vgl. mit Abb. 3.8, Abb. 3.20 und Abb. 4.8.
. Vgl. mit Abb. 3.8, Abb. 3.20 und Abb. 4.8.
|
|




Nächste Seite: Sekundäre
Bjerkneskraft bei hohem Aufwärts: Ergebnisse der numerischen Simulationen Vorherige Seite: Ergebnisse der numerischen Simulationen
Inhalt
Stefan Kamphausen 2003-07-17
![\includegraphics [width=8.5cm]{100_250/fb_100_0.01.ps}](img349.png)
![\includegraphics [width=6.791cm]{100_250/fb_100_0.01_sig.ps}](img350.png)
![\includegraphics [width=8.5cm]{100_250/fb_100_0.01.ps}](img349.png)
![\includegraphics [width=6.791cm]{100_250/fb_100_0.01_sig.ps}](img350.png)
![\includegraphics [width=8.5cm]{100_250/fb_50_0.01.ps}](img355.png)
![\includegraphics [width=6.791cm]{100_250/fb_50_0.01_sig.ps}](img356.png)
![]() in Abbildung 4.2 findet
sich dagegen wieder das gewohnte Bild wie in der entsprechenden Abbildung 3.14. Die Grenzen der ausgezeichneten Flächen
sind etwas ,,angeknabbert``, und durch eine hier benutzte Interpolation (es wurde nur
ein Drittel der Daten berechnet, die beim linearisierten Modell vorhanden waren)
etwas verschwommen. Am Rand der dargestellten Ebene lässt sich nicht mehr
interpolieren, was dazu führt, dass dort die Felder gleichen Vorzeichens scharf
begrenzt sind. Dies fällt nur bei genauem Hinsehen auf. Das Ergebnis stimmt gut
mit dem aus Abbildung 3.14 überein bis
auf einen kleinen Bereich in der Mitte, in dem eine (zur Winkelhalbierenden
symmetrische) Unregelmäßigkeit sichtbar wird. Auch die Verschiebung der
vorzeichenwechselnden Ruheradien zu höheren Werten gegenüber dem nicht
gekoppelten Fall wird hier durch das volle Modell bestätigt, sowie die
Entwicklung bei größerem Delay, die Annäherung an die nicht
gekoppelten Werte in der Nähe von
in Abbildung 4.2 findet
sich dagegen wieder das gewohnte Bild wie in der entsprechenden Abbildung 3.14. Die Grenzen der ausgezeichneten Flächen
sind etwas ,,angeknabbert``, und durch eine hier benutzte Interpolation (es wurde nur
ein Drittel der Daten berechnet, die beim linearisierten Modell vorhanden waren)
etwas verschwommen. Am Rand der dargestellten Ebene lässt sich nicht mehr
interpolieren, was dazu führt, dass dort die Felder gleichen Vorzeichens scharf
begrenzt sind. Dies fällt nur bei genauem Hinsehen auf. Das Ergebnis stimmt gut
mit dem aus Abbildung 3.14 überein bis
auf einen kleinen Bereich in der Mitte, in dem eine (zur Winkelhalbierenden
symmetrische) Unregelmäßigkeit sichtbar wird. Auch die Verschiebung der
vorzeichenwechselnden Ruheradien zu höheren Werten gegenüber dem nicht
gekoppelten Fall wird hier durch das volle Modell bestätigt, sowie die
Entwicklung bei größerem Delay, die Annäherung an die nicht
gekoppelten Werte in der Nähe von
![]() , bei
, bei ![]() in Abbildung 4.3.
in Abbildung 4.3.![]() -Werten näher an
-Werten näher an ![]() . Auch dieses findet sich im
nichtlinearen Modell bestätigt, wie man durch Vergleich der Abbildung 4.3 mit den Abbildungen aus der linearen
Näherung 3.2 (ungekoppelt)
und 3.15 (gekoppelt) feststellt.
. Auch dieses findet sich im
nichtlinearen Modell bestätigt, wie man durch Vergleich der Abbildung 4.3 mit den Abbildungen aus der linearen
Näherung 3.2 (ungekoppelt)
und 3.15 (gekoppelt) feststellt.![\includegraphics [width=8.5cm]{100_250/fb_10_0.01.ps}](img359.png)
![\includegraphics [width=6.791cm]{100_250/fb_10_0.01_sig.ps}](img360.png)
![\includegraphics [width=8.5cm]{100_250/fb_5_0.01.ps}](img361.png)
![\includegraphics [width=6.791cm]{100_250/fb_5_0.01_sig.ps}](img362.png)
![]() bis
bis ![]() zeigen, erkennt man das aus der linearen Theorie vorhergesagte Verhalten wieder.
Lediglich einige kleine Unregelmäßigkeiten sind in den Bildern zu sehen,
die zumeist den beginnenden Einfluss der Nichtlinearitäten wiederspiegeln. Sie
ließen sich auch durch eine längere Einschwingphase nicht bereinigen, so
dass man davon ausgehen darf, dass die weiterhin sichtbaren Effekte durch die
Nichtlinearität hervorgerufen werden. Sie ändern jedoch nichts an der
groben Struktur der Muster. Wie gewohnt erhält man für
zeigen, erkennt man das aus der linearen Theorie vorhergesagte Verhalten wieder.
Lediglich einige kleine Unregelmäßigkeiten sind in den Bildern zu sehen,
die zumeist den beginnenden Einfluss der Nichtlinearitäten wiederspiegeln. Sie
ließen sich auch durch eine längere Einschwingphase nicht bereinigen, so
dass man davon ausgehen darf, dass die weiterhin sichtbaren Effekte durch die
Nichtlinearität hervorgerufen werden. Sie ändern jedoch nichts an der
groben Struktur der Muster. Wie gewohnt erhält man für ![]() in
Abbildung 4.6 die durch die
Winkelhalbierende geteilte
in
Abbildung 4.6 die durch die
Winkelhalbierende geteilte ![]() -
-![]() -Ebene (hier mit zusätzlichen Mustern in der Nähe
des Vorzeichenwechsels) und bei
-Ebene (hier mit zusätzlichen Mustern in der Nähe
des Vorzeichenwechsels) und bei ![]() die umgekehrten Vorzeichen.
die umgekehrten Vorzeichen.![]() liegen die Gipfel noch bei hohen Ruheradien, bei
liegen die Gipfel noch bei hohen Ruheradien, bei ![]() bereits in der Nähe des Punktes, an dem beide Blasen einen Ruheradius beim
Resonanzradius haben, wobei von außen die charakteristischen Kämme
heranwachsen. Und bei allen größeren Abständen liegen die Extremwerte
in der Mitte.
bereits in der Nähe des Punktes, an dem beide Blasen einen Ruheradius beim
Resonanzradius haben, wobei von außen die charakteristischen Kämme
heranwachsen. Und bei allen größeren Abständen liegen die Extremwerte
in der Mitte.![\includegraphics [width=8.5cm]{100_250/fb_4.1_0.01.ps}](img363.png)
![\includegraphics [width=6.791cm]{100_250/fb_4.1_0.01_sig.ps}](img364.png)
![\includegraphics [width=8.5cm]{100_250/fb_4_0.01.ps}](img365.png)
![\includegraphics [width=6.791cm]{100_250/fb_4_0.01_sig.ps}](img366.png)
![\includegraphics [width=8.5cm]{100_250/fb_3_0.01.ps}](img367.png)
![\includegraphics [width=6.791cm]{100_250/fb_3_0.01_sig.ps}](img368.png)
![\includegraphics [width=8.5cm]{100_250/fb_2_0.01.ps}](img369.png)
![\includegraphics [width=6.791cm]{100_250/fb_2_0.01_sig.ps}](img370.png)
![]() -Werte bei einem anregenden Schallfeld von
-Werte bei einem anregenden Schallfeld von ![]() . Es wird also der
Fall betrachtet, bei dem die sekundären Bjerkneskräfte in der linearen
Näherung in Kapitel 3 dargestellt wurden.
Dieser Anregungsdruck liegt bei einem Druck, der die Linearisierbarkeit nicht mehr
unbedingt gewährleistet. Damit ist die Möglichkeit gegeben, die Grenzen der
Gültigkeit abzuschätzen. Es wurde gezeigt, dass für einen anregenden
Schalldruck von
. Es wird also der
Fall betrachtet, bei dem die sekundären Bjerkneskräfte in der linearen
Näherung in Kapitel 3 dargestellt wurden.
Dieser Anregungsdruck liegt bei einem Druck, der die Linearisierbarkeit nicht mehr
unbedingt gewährleistet. Damit ist die Möglichkeit gegeben, die Grenzen der
Gültigkeit abzuschätzen. Es wurde gezeigt, dass für einen anregenden
Schalldruck von ![]() , der im linearisierten Modell qualitativ die
gleichen Ergebnisse liefert wie ein höherer, da die Amplitude der Schwingung ja
linear (vgl. Gl. (3.11) und Gl. (3.25)) und somit die sekundäre Bjerkneskraft
quadratisch mit
, der im linearisierten Modell qualitativ die
gleichen Ergebnisse liefert wie ein höherer, da die Amplitude der Schwingung ja
linear (vgl. Gl. (3.11) und Gl. (3.25)) und somit die sekundäre Bjerkneskraft
quadratisch mit ![]() skaliert (vgl. Gl. (3.17),
in der der Druck nur in den Amplituden beider Blasen je einmal auftaucht), die
Ergebnisse aus der Linearisierung gut wiedergefunden werden konnten. Nun soll
untersucht werden, ob sich das bei einem höheren Schalldruck immer noch ergibt.
Die gezeigten Abbildungen sind also einerseits mit ihren Pendants aus der ersten
Serie dieses Abschnitts zu vergleichen, um den Effekt, den der höhere
Schalldruck bewirkt, zu studieren, andererseits mit denen aus Abschnitt 3.2.2, um den Einfluss der Nichtlinearitäten zu
betrachten.
skaliert (vgl. Gl. (3.17),
in der der Druck nur in den Amplituden beider Blasen je einmal auftaucht), die
Ergebnisse aus der Linearisierung gut wiedergefunden werden konnten. Nun soll
untersucht werden, ob sich das bei einem höheren Schalldruck immer noch ergibt.
Die gezeigten Abbildungen sind also einerseits mit ihren Pendants aus der ersten
Serie dieses Abschnitts zu vergleichen, um den Effekt, den der höhere
Schalldruck bewirkt, zu studieren, andererseits mit denen aus Abschnitt 3.2.2, um den Einfluss der Nichtlinearitäten zu
betrachten.![\includegraphics [width=8.5cm]{100_250/fb_100_0.1.ps}](img371.png)
![\includegraphics [width=6.791cm]{100_250/fb_100_0.1_sig.ps}](img372.png)
![]() erstaunlich, da die Verteilung der Vorzeichen so von der linearen Näherung
abweicht, dass die Linearisierbarkeit des Problems hier nicht gerechtfertigt scheint.
Die Form stimmt jedoch mit der aus Abbildung 4.1 sehr gut überein, wobei allerdings die
Größendordnung der Kraft in einem Bereich bei sehr großen Ruheradien
extrem zugenommen hat. Dabei gilt es zu beachten, dass sich die Blasen bei solchen
Ruheradien auf solche Werte aufziehen, dass sie sich beinahe berühren. Somit
darf keine sphärische Form mehr angenommen werden, was sowohl im
Keller-Miksis-Modell als auch bei der Berechnung der sekundären Bjerkneskraft
vorrausgesetzt wurde. Es wurden bei diesen Parametern auch Blasenpaare gefunden, die
sich gegenseitig extrem aufschaukeln und somit für die starken Kräfte in
diesem Modell verantwortlich sind. Die Lage der Vorzeichenwechsel stimmt dagegen
recht gut mit denen aus Abbildung 3.13
überein (etwa
erstaunlich, da die Verteilung der Vorzeichen so von der linearen Näherung
abweicht, dass die Linearisierbarkeit des Problems hier nicht gerechtfertigt scheint.
Die Form stimmt jedoch mit der aus Abbildung 4.1 sehr gut überein, wobei allerdings die
Größendordnung der Kraft in einem Bereich bei sehr großen Ruheradien
extrem zugenommen hat. Dabei gilt es zu beachten, dass sich die Blasen bei solchen
Ruheradien auf solche Werte aufziehen, dass sie sich beinahe berühren. Somit
darf keine sphärische Form mehr angenommen werden, was sowohl im
Keller-Miksis-Modell als auch bei der Berechnung der sekundären Bjerkneskraft
vorrausgesetzt wurde. Es wurden bei diesen Parametern auch Blasenpaare gefunden, die
sich gegenseitig extrem aufschaukeln und somit für die starken Kräfte in
diesem Modell verantwortlich sind. Die Lage der Vorzeichenwechsel stimmt dagegen
recht gut mit denen aus Abbildung 3.13
überein (etwa
![]() ). Sie hat sich durch den höheren Druck gegenüber der
ersten Serie in diesem Abschnitt nicht verändert (vgl. Abb. 4.1).
). Sie hat sich durch den höheren Druck gegenüber der
ersten Serie in diesem Abschnitt nicht verändert (vgl. Abb. 4.1).![\includegraphics [width=8.5cm]{100_250/fb_50_0.1.ps}](img373.png)
![\includegraphics [width=6.791cm]{100_250/fb_50_0.1_sig.ps}](img374.png)
![]() liegen diese Werte
sogar deutlich unter denen aus Abschnitt 3.2.2: unter
liegen diese Werte
sogar deutlich unter denen aus Abschnitt 3.2.2: unter
![]() gegenüber mehr als
gegenüber mehr als
![]() . Dies ist ein Anzeichen für das Verlassen der linearen
Näherung bei einem anregenden Schalldruck von
. Dies ist ein Anzeichen für das Verlassen der linearen
Näherung bei einem anregenden Schalldruck von ![]() . Hinzu kommt, dass der
Betrag der Kraft durchgehend höher ist. Wie bereits erwähnt kann der Betrag
um Größenordnungen zunehmen, wenn die Blasenschwingung die lineare
Domäne verlässt. Im Gebirgsplot der sekundären Bjerkneskraft in
Abbildung 4.10 fällt zudem der starke
Knick auf, der in Resonanzkurven (und die sekundäre Bjerkneskraft folgt diesen
ja in weiten Teilen; s. Abschnitt 3.2.1)
ein Zeichen für das Anwachsen einer Nichtlinearität ist. Genaugenommen
hängen die Resonanzkurven hier über und es gibt zwei verschiedene stabile
Lösungen (Hysterese; s. [21]).
. Hinzu kommt, dass der
Betrag der Kraft durchgehend höher ist. Wie bereits erwähnt kann der Betrag
um Größenordnungen zunehmen, wenn die Blasenschwingung die lineare
Domäne verlässt. Im Gebirgsplot der sekundären Bjerkneskraft in
Abbildung 4.10 fällt zudem der starke
Knick auf, der in Resonanzkurven (und die sekundäre Bjerkneskraft folgt diesen
ja in weiten Teilen; s. Abschnitt 3.2.1)
ein Zeichen für das Anwachsen einer Nichtlinearität ist. Genaugenommen
hängen die Resonanzkurven hier über und es gibt zwei verschiedene stabile
Lösungen (Hysterese; s. [21]).![\includegraphics [width=8.5cm]{100_250/fb_10_0.1.ps}](img376.png)
![\includegraphics [width=6.791cm]{100_250/fb_10_0.1_sig.ps}](img377.png)
![\includegraphics [width=8.5cm]{100_250/fb_5_0.1.ps}](img378.png)
![\includegraphics [width=6.791cm]{100_250/fb_5_0.1_sig.ps}](img379.png)
![]() zeigt
wieder die gewohnte Geometrie der Vorzeichenverteilung, bei allerdings kleineren
vorzeichenwechselnden Ruheradien. Die nichtlinearen Effekte sind hier nicht
ausschlaggebend. Gleiches gilt für Abbildung 4.12 bei
zeigt
wieder die gewohnte Geometrie der Vorzeichenverteilung, bei allerdings kleineren
vorzeichenwechselnden Ruheradien. Die nichtlinearen Effekte sind hier nicht
ausschlaggebend. Gleiches gilt für Abbildung 4.12 bei ![]() und Abbildung 4.13 bei
und Abbildung 4.13 bei ![]() .
.![\includegraphics [width=8.5cm]{100_250/fb_4.1_0.1.ps}](img380.png)
![\includegraphics [width=6.791cm]{100_250/fb_4.1_0.1_sig.ps}](img381.png)
![]() , der in Abbildung 4.14
dargestellt ist, offenbart dann wieder eine Abweichung vom Ergebnis der linearen
Näherung. Bei Ruheradien zwischen
, der in Abbildung 4.14
dargestellt ist, offenbart dann wieder eine Abweichung vom Ergebnis der linearen
Näherung. Bei Ruheradien zwischen
![]() und
und
![]() biegt die Grenze der Flächen gleichen Vorzeichens ab und
verlässt die Winkelhalbierende. Hier lassen sich nun auch Blasen finden, die
sich bei gleichem Ruheradius gegenseitig abstoßen.
biegt die Grenze der Flächen gleichen Vorzeichens ab und
verlässt die Winkelhalbierende. Hier lassen sich nun auch Blasen finden, die
sich bei gleichem Ruheradius gegenseitig abstoßen.![\includegraphics [width=8.5cm]{100_250/fb_4_0.1.ps}](img384.png)
![\includegraphics [width=6.791cm]{100_250/fb_4_0.1_sig.ps}](img385.png)
![\includegraphics [width=8.5cm]{100_250/fb_3_0.1.ps}](img386.png)
![\includegraphics [width=6.791cm]{100_250/fb_3_0.1_sig.ps}](img387.png)
![\includegraphics [width=8.5cm]{100_250/fb_2_0.1.ps}](img388.png)
![\includegraphics [width=6.791cm]{100_250/fb_2_0.1_sig.ps}](img389.png)